Wednesday, October 3, 2012
Sunday, September 30, 2012
While travelling in a cycle race, there are several pit stops. A cyclist can travel upto 50 km without stopping at any pit stop, where he can have a health drink and refill his energy. Given a start point ’t’ and let ’k’ be the distance needed to be travelled by the cyclist, find an efficient algorithm to reach the destination ’d’ so as to have minimum pit stops and prove your algorithm is the most optimal one.
Labels:Data
Microsoft Interview
You have given n numbers from 1 to n. You have to sort numbers with increasing number of set bits.
for ex: n=5.
output: 1,2,4,3,5
Note: If you have two number with equal number of set bits, then number with lowest value come first in the output.
output: 1,2,4,3,5
Note: If you have two number with equal number of set bits, then number with lowest value come first in the output.
Labels:Data
Microsoft Interview
Wednesday, September 26, 2012
Monday, September 24, 2012
You have N computers and [Ca, Cb] means a is connected to b and this connectivity is symmetric and transitive. then write a program which checks that all computers are interconnected and talk two each other
I Believe there are multiple way to solve this problem
1. Here is my approach since graph is connected there will be path from each source to destination vertex , isn't it ?
so we can simply run a dfs or bfs for all computers to check if all such path exist , finally we can return & of all operation that means all computer are inter connected and can talk to each other .
PS.Since graph is undirected if there exist path from u to v then vice-verse also true so we wont calculate it again.
Labels:Data
Adobe Question
,
Google Interview
Sunday, September 23, 2012
Maximum Sum Subsequence in an unsorted array of size n
We are given an array A having n integers. What we want to find is a contiguous subseqnence (A[i], A[i+1], …, A[j]) such that the sum of the elements in that subsequence is maximized. (Note that, in general, there may be more than one such optimal subsequence.)
Note that if all elements in A are non-negative, we could directly return the entire array as the required optimal subsequence.
APPROACH 1
A simple brute-force method could be to compute the sums of all possible subseqnences in A. How many subsequences are there? There are 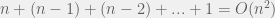 possible subsequences. Computing the sum of a subsequence takes O(n) in the worst-case. Hence, the running time of the algorithm would be
possible subsequences. Computing the sum of a subsequence takes O(n) in the worst-case. Hence, the running time of the algorithm would be  .
.
In C++, we could write the following function to do what was explained above:
// start and end are the starting and ending indices of an optimal subsequence.
void f ( int* A, int n, int &start, int& end)
{
int sum, max = A[0];
for (int i = 0; i < n ; i++)
for (int j = i; j < n; j++)
{
sum = 0;
for (int k = i; k <=j; k++)
sum+= A[k];
if (sum >= max)
{
start = i;
end = j;
max = sum;
}
}
}
————
APPROACH 2:
We can improve the running time to 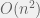 by being a bit more clever in computing the sums of different subsequences. We observe that the sum of the subsequence A[i ... j+1] = A[j+1] + sum of the subsequence A[i ... j].
by being a bit more clever in computing the sums of different subsequences. We observe that the sum of the subsequence A[i ... j+1] = A[j+1] + sum of the subsequence A[i ... j].
In C++, we could write as follows:
void f (int *A, int n, int &start, int &end)
{
int sum, max = A[0];
for (int i = 0; i < n; i++)
{
sum = 0;
for (int j = i; j < n; j++)
{
sum + = A[j];
if (sum >= max)
{
start = i;
end = j;
max = sum;
}
}
}
}
———–
APPROACH 3:
Using dynamic programming, we can solve the problem in linear time.
We consider a linear number of subproblems, each of which can be solved using previously solved subproblems in constant time, this giving a running time of  .
.
Let ![S[k] S[k]](http://s0.wp.com/latex.php?latex=S%5Bk%5D&bg=f0f0f0&fg=555555&s=0) denote the sum of a maximum sum contiguous subsequence ending exactly at index
denote the sum of a maximum sum contiguous subsequence ending exactly at index  .
.
Thus, we have that:
Also, S[0] = A[0].
——–
Using the above recurrence relation, we can compute the sum of the optimal subsequence for array A, which would just be the maximum over ![S[i] S[i]](http://s0.wp.com/latex.php?latex=S%5Bi%5D&bg=f0f0f0&fg=555555&s=0) for
for  .
.
Since we are required to output the starting and ending indices of an optimal subsequence, we would use another array  where
where ![T[i] T[i]](http://s0.wp.com/latex.php?latex=T%5Bi%5D&bg=f0f0f0&fg=555555&s=0) would store the starting index for a maximum sum contiguous subsequence ending at index i.
would store the starting index for a maximum sum contiguous subsequence ending at index i.
In prseducode form, the algorithm would look thus:
Create arrays S and T each of size n.
S[0] = A[0];
T[0] = 0;
max = S[0];
max_start = 0, max_end = 0;
For i going from 1 to n-1:
// We know that S[i] = max { S[i-1] + A[i], A[i] .
If ( S[i-1] > 0)
S[i] = S[i-1] + A[i];
T[i] = T[i-1];
Else
S[i] = A[i];
T[i] = i;
If ( S[i] > max)
max_start = T[i];
max_end = i;
max = S[i];
EndFor.
Output max_start and max_end.
———–
The above algorithm takes  time and
time and  space.
space.
——–
We can however improve upon the space requirements, reducing it to 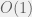 . The key idea is this: for computing S[i] and T[i], all we need are the values of S[i-1] and T[i-1] apart from the given array A. Hence, there is no need to store all
. The key idea is this: for computing S[i] and T[i], all we need are the values of S[i-1] and T[i-1] apart from the given array A. Hence, there is no need to store all 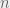 values of the S and T arrays.
values of the S and T arrays.
We could proceed as follows:
max = A[0];
max_start = 0;
max_end = 0;
S = A[0];
T = 0;
For i going from 1 to n-1:
// S = max { S + A[i], A[i] )
if ( S > 0)
S = S + A[i];
Else
S = A[i];
T = i;
If ( S > max)
max_start = T;
max_end = i;
max = S;
End For.
Output max_end and max_start.
———–
The above algorithm takes  time and
time and 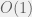 space.
space.
Labels:Data
Adobe Question
,
Amazon Interview
,
DirectI Interview
,
Dynamic Programming
,
Google Interview
,
Microsoft Interview
,
PocketGems
Saturday, September 15, 2012
How much tottal water can be stored in buildings
Given array of height 5 1 3 6 1 2
|
|..|
|..|
|.||
|.||.|
||||||
|
|..|
|..|
|.||
|.||.|
||||||
Labels:Data
DirectI Interview
Subscribe to:
Comments
(
Atom
)



