We are given an array A having n integers. What we want to find is a contiguous subseqnence (A[i], A[i+1], …, A[j]) such that the sum of the elements in that subsequence is maximized. (Note that, in general, there may be more than one such optimal subsequence.)
Note that if all elements in A are non-negative, we could directly return the entire array as the required optimal subsequence.
APPROACH 1
A simple brute-force method could be to compute the sums of all possible subseqnences in A. How many subsequences are there? There are
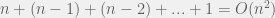
possible subsequences. Computing the sum of a subsequence takes O(n) in the worst-case. Hence, the running time of the algorithm would be

.
In C++, we could write the following function to do what was explained above:
// start and end are the starting and ending indices of an optimal subsequence.
void f ( int* A, int n, int &start, int& end)
{
int sum, max = A[0];
for (int i = 0; i < n ; i++)
for (int j = i; j < n; j++)
{
sum = 0;
for (int k = i; k <=j; k++)
sum+= A[k];
if (sum >= max)
{
start = i;
end = j;
max = sum;
}
}
}
————
APPROACH 2:
We can improve the running time to
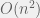
by being a bit more clever in computing the sums of different subsequences. We observe that the sum of the subsequence A[i ... j+1] = A[j+1] + sum of the subsequence A[i ... j].
In C++, we could write as follows:
void f (int *A, int n, int &start, int &end)
{
int sum, max = A[0];
for (int i = 0; i < n; i++)
{
sum = 0;
for (int j = i; j < n; j++)
{
sum + = A[j];
if (sum >= max)
{
start = i;
end = j;
max = sum;
}
}
}
}
———–
APPROACH 3:
Using dynamic programming, we can solve the problem in linear time.
We consider a linear number of subproblems, each of which can be solved using previously solved subproblems in constant time, this giving a running time of

.
Let
![S[k] S[k]](http://s0.wp.com/latex.php?latex=S%5Bk%5D&bg=f0f0f0&fg=555555&s=0)
denote the sum of a maximum sum contiguous subsequence ending exactly at index

.
Thus, we have that:
![S[k+1] = max \{S[k] + A[k+1], A[k+1] \} S[k+1] = max \{S[k] + A[k+1], A[k+1] \}](http://s0.wp.com/latex.php?latex=S%5Bk%2B1%5D+%3D+max+%5C%7BS%5Bk%5D+%2B+A%5Bk%2B1%5D%2C+A%5Bk%2B1%5D+%5C%7D&bg=f0f0f0&fg=555555&s=0)
(for all
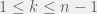
)
Also, S[0] = A[0].
——–
Using the above recurrence relation, we can compute the sum of the optimal subsequence for array A, which would just be the maximum over
![S[i] S[i]](http://s0.wp.com/latex.php?latex=S%5Bi%5D&bg=f0f0f0&fg=555555&s=0)
for

.
Since we are required to output the starting and ending indices of an optimal subsequence, we would use another array

where
![T[i] T[i]](http://s0.wp.com/latex.php?latex=T%5Bi%5D&bg=f0f0f0&fg=555555&s=0)
would store the starting index for a maximum sum contiguous subsequence ending at index i.
In prseducode form, the algorithm would look thus:
Create arrays S and T each of size n.
S[0] = A[0];
T[0] = 0;
max = S[0];
max_start = 0, max_end = 0;
For i going from 1 to n-1:
// We know that S[i] = max { S[i-1] + A[i], A[i] .
If ( S[i-1] > 0)
S[i] = S[i-1] + A[i];
T[i] = T[i-1];
Else
S[i] = A[i];
T[i] = i;
If ( S[i] > max)
max_start = T[i];
max_end = i;
max = S[i];
EndFor.
Output max_start and max_end.
———–
The above algorithm takes

time and

space.
——–
We can however improve upon the space requirements, reducing it to
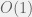
. The key idea is this: for computing S[i] and T[i], all we need are the values of S[i-1] and T[i-1] apart from the given array A. Hence, there is no need to store all
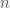
values of the S and T arrays.
We could proceed as follows:
max = A[0];
max_start = 0;
max_end = 0;
S = A[0];
T = 0;
For i going from 1 to n-1:
// S = max { S + A[i], A[i] )
if ( S > 0)
S = S + A[i];
Else
S = A[i];
T = i;
If ( S > max)
max_start = T;
max_end = i;
max = S;
End For.
Output max_end and max_start.
———–
The above algorithm takes

time and
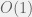
space.



