Sunday, September 30, 2012
While travelling in a cycle race, there are several pit stops. A cyclist can travel upto 50 km without stopping at any pit stop, where he can have a health drink and refill his energy. Given a start point ’t’ and let ’k’ be the distance needed to be travelled by the cyclist, find an efficient algorithm to reach the destination ’d’ so as to have minimum pit stops and prove your algorithm is the most optimal one.
Labels:Data
Microsoft Interview
You have given n numbers from 1 to n. You have to sort numbers with increasing number of set bits.
for ex: n=5.
output: 1,2,4,3,5
Note: If you have two number with equal number of set bits, then number with lowest value come first in the output.
output: 1,2,4,3,5
Note: If you have two number with equal number of set bits, then number with lowest value come first in the output.
Labels:Data
Microsoft Interview
Wednesday, September 26, 2012
Monday, September 24, 2012
You have N computers and [Ca, Cb] means a is connected to b and this connectivity is symmetric and transitive. then write a program which checks that all computers are interconnected and talk two each other
I Believe there are multiple way to solve this problem
1. Here is my approach since graph is connected there will be path from each source to destination vertex , isn't it ?
so we can simply run a dfs or bfs for all computers to check if all such path exist , finally we can return & of all operation that means all computer are inter connected and can talk to each other .
PS.Since graph is undirected if there exist path from u to v then vice-verse also true so we wont calculate it again.
Labels:Data
Adobe Question
,
Google Interview
Sunday, September 23, 2012
Maximum Sum Subsequence in an unsorted array of size n
We are given an array A having n integers. What we want to find is a contiguous subseqnence (A[i], A[i+1], …, A[j]) such that the sum of the elements in that subsequence is maximized. (Note that, in general, there may be more than one such optimal subsequence.)
Note that if all elements in A are non-negative, we could directly return the entire array as the required optimal subsequence.
APPROACH 1
A simple brute-force method could be to compute the sums of all possible subseqnences in A. How many subsequences are there? There are 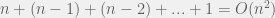 possible subsequences. Computing the sum of a subsequence takes O(n) in the worst-case. Hence, the running time of the algorithm would be
possible subsequences. Computing the sum of a subsequence takes O(n) in the worst-case. Hence, the running time of the algorithm would be  .
.
In C++, we could write the following function to do what was explained above:
// start and end are the starting and ending indices of an optimal subsequence.
void f ( int* A, int n, int &start, int& end)
{
int sum, max = A[0];
for (int i = 0; i < n ; i++)
for (int j = i; j < n; j++)
{
sum = 0;
for (int k = i; k <=j; k++)
sum+= A[k];
if (sum >= max)
{
start = i;
end = j;
max = sum;
}
}
}
————
APPROACH 2:
We can improve the running time to 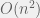 by being a bit more clever in computing the sums of different subsequences. We observe that the sum of the subsequence A[i ... j+1] = A[j+1] + sum of the subsequence A[i ... j].
by being a bit more clever in computing the sums of different subsequences. We observe that the sum of the subsequence A[i ... j+1] = A[j+1] + sum of the subsequence A[i ... j].
In C++, we could write as follows:
void f (int *A, int n, int &start, int &end)
{
int sum, max = A[0];
for (int i = 0; i < n; i++)
{
sum = 0;
for (int j = i; j < n; j++)
{
sum + = A[j];
if (sum >= max)
{
start = i;
end = j;
max = sum;
}
}
}
}
———–
APPROACH 3:
Using dynamic programming, we can solve the problem in linear time.
We consider a linear number of subproblems, each of which can be solved using previously solved subproblems in constant time, this giving a running time of  .
.
Let ![S[k] S[k]](http://s0.wp.com/latex.php?latex=S%5Bk%5D&bg=f0f0f0&fg=555555&s=0) denote the sum of a maximum sum contiguous subsequence ending exactly at index
denote the sum of a maximum sum contiguous subsequence ending exactly at index  .
.
Thus, we have that:
Also, S[0] = A[0].
——–
Using the above recurrence relation, we can compute the sum of the optimal subsequence for array A, which would just be the maximum over ![S[i] S[i]](http://s0.wp.com/latex.php?latex=S%5Bi%5D&bg=f0f0f0&fg=555555&s=0) for
for  .
.
Since we are required to output the starting and ending indices of an optimal subsequence, we would use another array  where
where ![T[i] T[i]](http://s0.wp.com/latex.php?latex=T%5Bi%5D&bg=f0f0f0&fg=555555&s=0) would store the starting index for a maximum sum contiguous subsequence ending at index i.
would store the starting index for a maximum sum contiguous subsequence ending at index i.
In prseducode form, the algorithm would look thus:
Create arrays S and T each of size n.
S[0] = A[0];
T[0] = 0;
max = S[0];
max_start = 0, max_end = 0;
For i going from 1 to n-1:
// We know that S[i] = max { S[i-1] + A[i], A[i] .
If ( S[i-1] > 0)
S[i] = S[i-1] + A[i];
T[i] = T[i-1];
Else
S[i] = A[i];
T[i] = i;
If ( S[i] > max)
max_start = T[i];
max_end = i;
max = S[i];
EndFor.
Output max_start and max_end.
———–
The above algorithm takes  time and
time and  space.
space.
——–
We can however improve upon the space requirements, reducing it to 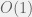 . The key idea is this: for computing S[i] and T[i], all we need are the values of S[i-1] and T[i-1] apart from the given array A. Hence, there is no need to store all
. The key idea is this: for computing S[i] and T[i], all we need are the values of S[i-1] and T[i-1] apart from the given array A. Hence, there is no need to store all 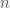 values of the S and T arrays.
values of the S and T arrays.
We could proceed as follows:
max = A[0];
max_start = 0;
max_end = 0;
S = A[0];
T = 0;
For i going from 1 to n-1:
// S = max { S + A[i], A[i] )
if ( S > 0)
S = S + A[i];
Else
S = A[i];
T = i;
If ( S > max)
max_start = T;
max_end = i;
max = S;
End For.
Output max_end and max_start.
———–
The above algorithm takes  time and
time and 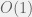 space.
space.
Labels:Data
Adobe Question
,
Amazon Interview
,
DirectI Interview
,
Dynamic Programming
,
Google Interview
,
Microsoft Interview
,
PocketGems
Saturday, September 15, 2012
How much tottal water can be stored in buildings
Given array of height 5 1 3 6 1 2
|
|..|
|..|
|.||
|.||.|
||||||
|
|..|
|..|
|.||
|.||.|
||||||
Labels:Data
DirectI Interview
Tuesday, September 4, 2012
A Short Tutorial on Recurrence Relations
The concept: Recurrence relations are recursive definitions of
mathematical functions or sequences. For example, the recurrence
relation
g(n) = g(n-1) + 2n -1
g(0) = 0
defines the function f(n) = n^2, and the recurrence relation
f(n) = f(n-1) + f(n-2)
f(1) = 1
f(0) = 1
defines the famous Fibanocci sequence 1,1,2,3,5,8,13,....
Solving a recurrence relation: Given a function defined by a recurrence
relation, we want to find a "closed form" of the function. In other words,
we would like to eliminate recursion from the function definition.
There are several techniques for solving recurrence relations.
The main techniques for us are the iteration method (also called expansion,
or unfolding methods) and the Master Theorem method. Here is an example
of solving the above recurrence relation for g(n) using the iteration
method:
g(n) = g(n-1) + 2n - 1
= [g(n-2) + 2(n-1) - 1] + 2n - 1
// because g(n-1) = g(n-2) + 2(n-1) -1 //
= g(n-2) + 2(n-1) + 2n - 2
= [g(n-3) + 2(n-2) -1] + 2(n-1) + 2n - 2
// because g(n-2) = g(n-3) + 2(n-2) -1 //
= g(n-3) + 2(n-2) + 2(n-1) + 2n - 3
...
= g(n-i) + 2(n-i+1) +...+ 2n - i
...
= g(n-n) + 2(n-n+1) +...+ 2n - n
= 0 + 2 + 4 +...+ 2n - n
// because g(0) = 0 //
= 2 + 4 +...+ 2n - n
= 2*n*(n+1)/2 - n
// using arithmetic progression formula 1+...+n = n(n+1)/2 //
= n^2
Applications: Recurrence relations are a fundamental mathematical
tool since they can be used to represent mathematical functions/sequences
that cannot be easily represented non-recursively. An example
is the Fibanocci sequence. Another one is the famous Ackermann's
function that you may (or may not :-) have heard about in Math112 or
CS14 [see CLR, pp. 451-453]. Here we are mainly interested in applications
of recurrence relations in the design and analysis of algorithms.
Recurrence relations with more than one variable: In some applications
we may consider recurrence relations with two or more variables. The
famous Ackermann's function is one such example. Here is another example
recurrence relation with two variables.
T(m,n) = 2*T(m/2,n/2) + m*n, m > 1, n > 1
T(m,n) = n, if m = 1
T(m,n) = m, if n = 1
We can solve this recurrence using the iteration method as follows.
Assume m <= n. Then
T(m,n) = 2*T(m/2,n/2) + m*n
= 2^2*T(m/2^2,n/2^2) + 2*(m*n/4) + m*n
= 2^2*T(m/2^2,n/2^2) + m*n/2 + m*n
= 2^3*T(m/2^3,n/2^3) + m*n/2^2 + m*n/2 + m*n
...
= 2^i*T(m/2^i,n/2^i) + m*n/2^(i-1) +...+ m*n/2^2 + m*n/2 + m*n
Let k = log_2 m. Then we have
T(m,n) = 2^k*T(m/2^k,n/2^k) + m*n/2^(k-1) +...+ m*n/2^2 + m*n/2 + m*n
= m*T(m/m,n/2^k) + m*n/2^(k-1) +...+ m*n/2^2 + m*n/2 + m*n
= m*T(1,n/2^k) + m*n/2^(k-1) +...+ m*n/2^2 + m*n/2 + m*n
= m*n/2^k + m*n/2^(k-1) +...+ m*n/2^2 + m*n/2 + m*n
= m*n*(2-1/2^k)
= Theta(m*n)
Analyzing (recursive) algorithms using recurrence relations: For recursive
algorithms, it is convinient to use recurrence relations to describe
the time complexity functions of the algorithms. Then we can obtain
the time complexity estimates by solving the recurrence relations. You
may find several examples of this nature in the lecture notes and the books,
such as Towers of Hanoi, Mergesort (the recursive version), and Majority.
These are excellent examples of divide-and-conquer algorithms whose
analyses involve recurrence relations.
Here is another example. Given algorithm
Algorithm Test(A[1..n], B[1..n], C[1..n]);
if n= 0 then return;
For i := 1 to n do
C[1] := A[1] * B[i];
call Test(A[2..n], B[2..n], C[2..n]);
If the denote the time complexity of Test as T(n), then we can express T(n)
recursively as an recurrence relation:
T(n) = T(n-1) + O(n)
T(1) = 1
(You may also write simply T(n) = T(n-1) + n if you think of T(n)
as the the number of multiplications)
By a straighforward expansion method, we can solve T(n) as:
T(n) = T(n-1) + O(n)
= (T(n-2) + O(n-1)) + O(n)
= T(n-2) + O(n-1) + O(n)
= T(n-3) + O(n-2) + O(n-1) + O(n)
...
= T(1) + O(2) + ... + O(n-1) + O(n)
= O(1 + 2 + ... + n-1 + n)
= O(n^2)
Yet another example:
Algorithm Parallel-Product(A[1..n]);
if n = 1 then return;
for i := 1 to n/2 do
A[i] := A[i]*A[i+n/2];
call Parallel-Product(A[1..n/2]);
The time complexity of the above algorithm can be expressed as
T(n) = T(n/2) + O(n/2)
T(1) = 1
We can solve it as:
T(n) = T(n/2) + O(n/2)
= (T(n/2^2) + O(n/2^2)) + O(n/2)
= T(n/2^2) + O(n/2^2) + O(n/2)
= T(n/2^3) + O(n/2^3) + O(n/2^2) + O(n/2)
...
= T(n/2^i) + O(n/2^i) +...+ O(n/2^2) + O(n/2)
= T(n/2^log n) + O(n/2^log n) +...+ O(n/2^2) + O(n/2)
// We stop the expansion at i = log n because
2^log n = n //
= T(1) + O(n/2^log n) +...+ O(n/2^2) + O(n/2)
= 1 + O(n/2^log n +...+ n/2^2 + n/2)
= 1 + O(n*(1/2^log n +...+ 1/2^2 + 1/2)
= O(n)
// because 1/2^log n +...+ 1/2^2 + 1/2 <= 1 //
Using recurrence relations to develop algorithms: Recurrence relations are
useful in the design of algorithms, as in the dynamic programming paradigm.
For this course, you only need to know how to derive an iterative (dynamic
programming) algorithm when you are given a recurrence relation.
For example, given the recurrence relation for the Fibonacci function f(n)
above, we can convert it into DP algorithm as follows:
Algorithm Fib(n);
var f[0..n]: array of integers;
f[0] := f[1] := 1;
for i := 2 to n do
f[i] := f[i-1] + f[i-2];
// following the recurrence relation //
return f[n];
The time complexity of this algorithm is easily seen as O(n). Of course
you may also easily derive a recursive algorithm from the recurrence relation:
Algorithm Fib-Rec(n);
if n = 0 or 1 then return 1;
else
return Fib-Rec(n-1) + Fib-Rec(n-2);
but the time complexity of this algorithm will be exponential, since
we can write its time complexity function recursively as:
T(n) = T(n-1) + T(n-2)
T(1) = T(0) = 1
In other words, T(n) is exactly the n-th Fibonacci nummber. To solve this
recurrence relation, we would have to use a more sophisticated technique
for linear homogeneous recurrence relations, which is discussed in the
text book for Math112. But for us, here it suffices to know that
T(n) = f(n) = theta(c^n), where c is a constant close to 1.5.
Source : http://www.cs.ucr.edu/~jiang/cs141/recur-tut.txt
Labels:Data
Recursion
Subscribe to:
Comments
(
Atom
)



