Question: Given a 2D array / matrix of integers. Write a program to print the elements in spiral order. Consider a matrix as show in the diagram to the right. The desired output of the program should be as: 1,2,3,4,8,12,16,20,19,18,17,13,9,5,6, 7,11,15,14,10.

Solution: There are several ways to solve this problem, but I am mentioning a method that is intuitive to understand and easy to implement. The idea is to consider the matrix similar to onion which can be peeled layer after layer. We can use the same approach to print the outer layer of the matrix and keep doing it recursively on a smaller matrix (with 1 less row and 1 less column).
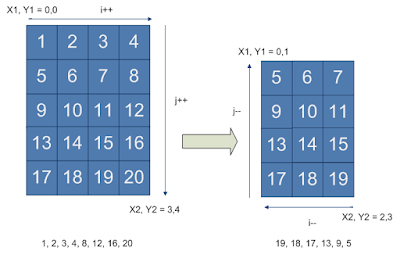
Refer to the image below for a visual explanation. We start by printing the top-right layer of the matrix by calling the print_layer_top_right. It will print 1,2,3,4,8,12,16,20. The print_layer_top_right method then calls the print_layer_bottom_left method which will print 19,18,17,13,9,5. If you observe the size of the target matrix is reducing after each call. Each method basically calls the other method and passes the matrix indexes for the reduced matrix. Both methods take 4 index parameters which represent the target matrix. When the target matrix size is such that there is only one layer left the recursion terminates and by this time the code has printed all the numbers in the full matrix.
Code (C language):
#include
void print_layer_top_right(int a[][4], int x1, int y1, int x2, int y2);
void print_layer_bottom_left(int a[][4], int x1, int y1, int x2, int y2);
int main(void)
{
int a[5][4] = {
{1,2,3,4},
{5,6,7,8},
{9,10,11,12},
{13,14,15,16},
{17,18,19,20}
};
print_layer_top_right(a,0,0,3,4);
}
//
// prints the top and right shells of the matrix
//
void print_layer_top_right(int a[][4], int x1, int y1, int x2, int y2)
{
int i = 0, j = 0;
// print the row
for(i = x1; i<=x2; i++)
{
printf("%d,", a[y1][i]);
}
//print the column
for(j = y1 + 1; j <= y2; j++)
{
printf("%d,", a[j][x2]);
}
// see if we have more cells left
if(x2-x1 > 0)
{
// 'recursively' call the function to print the bottom-left layer
print_layer_bottom_left(a, x1, y1 + 1, x2-1, y2);
}
}
//
// prints the bottom and left shells of the matrix
//
void print_layer_bottom_left(int a[][4], int x1, int y1, int x2, int y2)
{
int i = 0, j = 0;
//print the row of the matrix in reverse
for(i = x2; i>=x1; i--)
{
printf("%d,", a[y2][i]);
}
// print the last column of the matrix in reverse
for(j = y2 - 1; j >= y1; j--)
{
printf("%d,", a[j][x1]);
}
if(x2-x1 > 0)
{
// 'recursively' call the function to print the top-right layer
print_layer_top_right(a, x1+1, y1, x2, y2-1);
}
}

Solution: There are several ways to solve this problem, but I am mentioning a method that is intuitive to understand and easy to implement. The idea is to consider the matrix similar to onion which can be peeled layer after layer. We can use the same approach to print the outer layer of the matrix and keep doing it recursively on a smaller matrix (with 1 less row and 1 less column).
Refer to the image below for a visual explanation. We start by printing the top-right layer of the matrix by calling the print_layer_top_right. It will print 1,2,3,4,8,12,16,20. The print_layer_top_right method then calls the print_layer_bottom_left method which will print 19,18,17,13,9,5. If you observe the size of the target matrix is reducing after each call. Each method basically calls the other method and passes the matrix indexes for the reduced matrix. Both methods take 4 index parameters which represent the target matrix. When the target matrix size is such that there is only one layer left the recursion terminates and by this time the code has printed all the numbers in the full matrix.

Code (C language):
<script type="syntaxhighlighter" class="brush: html"><![CDATA[
#include
void print_layer_top_right(int a[][4], int x1, int y1, int x2, int y2);
void print_layer_bottom_left(int a[][4], int x1, int y1, int x2, int y2);
int main(void)
{
int a[5][4] = {
{1,2,3,4},
{5,6,7,8},
{9,10,11,12},
{13,14,15,16},
{17,18,19,20}
};
print_layer_top_right(a,0,0,3,4);
}
//
// prints the top and right shells of the matrix
//
void print_layer_top_right(int a[][4], int x1, int y1, int x2, int y2)
{
int i = 0, j = 0;
// print the row
for(i = x1; i<=x2; i++)
{
printf("%d,", a[y1][i]);
}
//print the column
for(j = y1 + 1; j <= y2; j++)
{
printf("%d,", a[j][x2]);
}
// see if we have more cells left
if(x2-x1 > 0)
{
// 'recursively' call the function to print the bottom-left layer
print_layer_bottom_left(a, x1, y1 + 1, x2-1, y2);
}
}
//
// prints the bottom and left shells of the matrix
//
void print_layer_bottom_left(int a[][4], int x1, int y1, int x2, int y2)
{
int i = 0, j = 0;
//print the row of the matrix in reverse
for(i = x2; i>=x1; i--)
{
printf("%d,", a[y2][i]);
}
// print the last column of the matrix in reverse
for(j = y2 - 1; j >= y1; j--)
{
printf("%d,", a[j][x1]);
}
if(x2-x1 > 0)
{
// 'recursively' call the function to print the top-right layer
print_layer_top_right(a, x1+1, y1, x2, y2-1);
}
}
]]></script>
Run Here https://ideone.com/ut0Hx
