Showing posts with label Hyves Interview. Show all posts
Showing posts with label Hyves Interview. Show all posts
Tuesday, November 29, 2011
Friday, September 16, 2011
Wednesday, August 24, 2011
Design an algorithm that takes strings S and r and returns if r matches s. (Assume r is a well-formed regular expression.)
Before starting solving we need to think about some test cases like .,*,?,^,$ e.g about a regular expression grammar.
A regular expression is a sequence of characters that defines a set of
matching strings.For this problem , we define a simple subset of a full
regular expression Language.
matching strings.For this problem , we define a simple subset of a full
regular expression Language.
Alphabetical and numerical characters match themselves.
1.For example aW9 will match that string of 3 letters wherever it appears.
The meta-characters ". and $ stand for the beginning and end of the
string. For example, .....aW9 matches aW9 only at the start of a string
aW9$ matches aW9 only at the end of a string, and ^aW9$ matches a string only if it is exactly equal to aW9.
string. For example, .....aW9 matches aW9 only at the start of a string
aW9$ matches aW9 only at the end of a string, and ^aW9$ matches a string only if it is exactly equal to aW9.
2.The metacharacter . matches any single character. For example,
a.9 matches a89 and xyaW9123 but not aw89.
3.The metacharacter * specifies a repetition of the single previous
period or a literal character. For example,a. *9 matches aw89.
By definition, regular expression r matches string s if s contains a
substring starting at any position matching r. For example, aW9 and a. 9
match string xyaW9123 but .....aW9 does not.
By definition, regular expression r matches string s if s contains a
substring starting at any position matching r. For example, aW9 and a. 9
match string xyaW9123 but .....aW9 does not.
Algorithm:
The key to solving this problem is using recursion effectively.
If the regular expression r starts with "', then s must match the remainder of r; otherwise, s must match r at some position.
If the regular expression r starts with "', then s must match the remainder of r; otherwise, s must match r at some position.
Call the function that checks whether a string S matches r from
the beginning matchHere. This function has to check several cases
the beginning matchHere. This function has to check several cases
(1.) Iength-O regular expressions which match everything,
(2.) a regular expression starting with a *match,
(3.) the regular expression $,and
(4.) a regular expression starting with an alphanumeric character or dot.
Of these, (1.) and (3.) are base cases, (4.) is a check followed by a call
to matchHere, and (3.) requires a new matchStar function.
More Info http://swtch.com/~rsc/regexp/regexp1.html
Of these, (1.) and (3.) are base cases, (4.) is a check followed by a call
to matchHere, and (3.) requires a new matchStar function.
More Info http://swtch.com/~rsc/regexp/regexp1.html
Labels:Data
DirectI Interview
,
Facebook Interview
,
Google Interview
,
Hyves Interview
Tuesday, August 23, 2011
Write a function int interval_unfold_count(int n); that returns the length of the shortest sequence of operations resulting in either L or R being equal to N.
Two integer variables L and R are initially equal to 0 and 1 respectively (i.e. L = 0 and R = 1).
The values of these variables can be manipulated using the following operations: operation 'L' is the assignment L = 2*L-R, operation 'R' is the assignment R = 2*R-L.
Given an integer N we want to find what is the shortest sequence of such operations necessary to make either L or R equal to N. For example, given N = 21, the following sequence of operations:
(initially L = 0, R = 1),
L = 2*L-R (makes L = -1, R = 1),
L = 2*L-R (makes L = -3, R = 1),
R = 2*R-L (makes L = -3, R = 5),
L = 2*L-R (makes L = -11, R = 5),
R = 2*R-L (makes L = -11, R = 21)
makes one of the variables (namely R) equal to N (i.e. after the last operation N = R = 21). This sequence consists of 5 operations and there is no shorter sequence that would make either L or R equal 21.
Write a function int interval_unfold_count(int n);
that returns the length of the shortest sequence of operations resulting in either L or R being equal to N. For example, given N = 21 the function should return 5.
The values of these variables can be manipulated using the following operations: operation 'L' is the assignment L = 2*L-R, operation 'R' is the assignment R = 2*R-L.
Given an integer N we want to find what is the shortest sequence of such operations necessary to make either L or R equal to N. For example, given N = 21, the following sequence of operations:
(initially L = 0, R = 1),
L = 2*L-R (makes L = -1, R = 1),
L = 2*L-R (makes L = -3, R = 1),
R = 2*R-L (makes L = -3, R = 5),
L = 2*L-R (makes L = -11, R = 5),
R = 2*R-L (makes L = -11, R = 21)
makes one of the variables (namely R) equal to N (i.e. after the last operation N = R = 21). This sequence consists of 5 operations and there is no shorter sequence that would make either L or R equal 21.
Write a function int interval_unfold_count(int n);
that returns the length of the shortest sequence of operations resulting in either L or R being equal to N. For example, given N = 21 the function should return 5.
Labels:Data
Amazon Interview
,
DirectI Interview
,
Hyves Interview
Saturday, August 6, 2011
Coin Denomination Problem
Let us say we have an amount we have to pay someone: say $97. The given currency has notes worth $1, $5, $10 and $50. Now, what is the minimum number of currency notes with which the amount can be made? In this case, its eight: two $1 notes, a $5 note, four $10 notes and a $50 notes - eight in all.
If a computer had to solve the same problem, how would it do it? Let us see below. ‘Denomination’ refers to the list of available currency notes: $1, $5, $10 and $50 in this case - each note is a denomination.
In General
Problem: We are given a set of denominations d1,d2,d3,...,dn in increasing order. (Without loss of generality) we assume also that d1=1 (that is, there is always a $1 note, and that is the first denomination) so that it is always possible to produce all amounts from the given denominations. We are also given an amount of money amt. We must use a minimum number of coins (or currency notes) of the given denominations to produce amt.
Great Info http://www.seeingwithc.org/topic1html.html
If a computer had to solve the same problem, how would it do it? Let us see below. ‘Denomination’ refers to the list of available currency notes: $1, $5, $10 and $50 in this case - each note is a denomination.
In General
Problem: We are given a set of denominations d1,d2,d3,...,dn in increasing order. (Without loss of generality) we assume also that d1=1 (that is, there is always a $1 note, and that is the first denomination) so that it is always possible to produce all amounts from the given denominations. We are also given an amount of money amt. We must use a minimum number of coins (or currency notes) of the given denominations to produce amt.
Great Info http://www.seeingwithc.org/topic1html.html
Saturday, July 16, 2011
How to Count Number of Set Bits e.g. Number of 1's efficiently ?
This Question is asked in almost all core s/w companies & most of we know logarithmic solution of this problem but there exist a constant time solution using bit manipulations stuck !!!!:) See 2nd Method to solve the same problem in O(1)
1st Brian Kernighan’s Algorithm:
Subtraction of 1 from a number toggles all the bits (from right to left) till the rightmost set bit(including the righmost set bit). So if we subtract a number by 1 and do bitwise & with itself (n & (n-1)), we unset the righmost set bit. If we do n & (n-1) in a loop and count the no of times loop executes we get the set bit count.
Beauty of the this solution is number of times it loops is equal to the number of set bits in a given integer.
1 Initialize count: = 0
2 If integer n is not zero
(a) Do bitwise & with (n-1) and assign the value back to n
n: = n&(n-1)
(b) Increment count by 1
(c) go to step 2
3 Else return count
#include
/* Function to get no of set bits in binary
representation of passed binary no. */
int countSetBits(int n)
{
unsigned int count = 0;
while (n)
{
n &= (n-1) ;
count++;
}
return count;
}
/* Program to test function countSetBits */
int main()
{
int i = 16;
printf("%d", countSetBits(i));
getchar();
return 0;
}
Time Complexity O(logn)
Space Complexity O(1)
Run Here https://ideone.com/2y2KJ
2nd Method is Most Efficient One !!!!!!
Assuming that the integer is 32 bits, this is pretty good:
x = (x & 0x55555555) + ((x >> 1) & 0x55555555);
x = (x & 0x33333333) + ((x >> 2) & 0x33333333);
x = (x & 0x0F0F0F0F) + ((x >> 4) & 0x0F0F0F0F);
x = (x & 0x00FF00FF) + ((x >> 8) & 0x00FF00FF);
x = (x & 0x0000FFFF) + ((x >> 16) & 0x0000FFFF);
where
0x55555555 = 01010101 01010101 01010101 01010101
0x33333333 = 00110011 00110011 00110011 00110011
0x0F0F0F0F = 00001111 00001111 00001111 00001111
0x00FF00FF = 00000000 11111111 00000000 11111111
0x0000FFFF = 00000000 00000000 11111111 11111111
Notice that the hex constants are respectively alternate bits,
alternate pairs of bits, alternate groups of four bits, alternate
bytes, and the low-order half of the int.
The first statement determines the number of one-bits in each pair of
bits. The second statement adds adjacent pairs of bits to get the
number of bits in each group of four bits. Then these are added to get
the number of bits in each byte, short int, and finally in the whole
int.
but it works at low level ??
Suppose that the first four bits of x from the left are abcd. Lets separate the bits into pairs with a comma: ab,cd. The first four bits of the hex constant0x55... are 0101, or separated into pairs: 01,01. The logical product of x with this constant is 0b,0d. The first four bits of x>>1 are 0abc, or separated into pairs are 0a,bc. The logical product of this with the constant is 0a,0c. The sum 0b,0d + 0a,0c is a+b,c+d, where a+b = 00, 01, or 10, and b+c = 00, 01, or 10. Thus we have replaced each pair of bits in x with the sum of the two bits originally in the pair.
The next statement uses the constant 0x333.... The first four bits of this are 0011, split into pairs as 00,11. The logical product of the first four bits of x with this constant gives 00,c+d. Furthermore (a+b,c+d)>>2 = 00,a+b. Then 00,c+d + 00,a+b gives the four-bit quantity a+b+c+d, i.e., the number of one bits set in the first four bits of the original x.
The next statements continue to double the number of bits included in each sum.
& so on
#include
using namespace std;
int main()
{
int x=0x00000016;
x = (x & 0x55555555) + ((x >> 1) & 0x55555555);
cout<> 2) & 0x33333333);
cout<> 4) & 0x0F0F0F0F);
cout<> 8) & 0x00FF00FF);
cout<> 16) & 0x0000FFFF);
cout<
return 0;
}
Time Complexity O(1)
Space Complexity O(1)
Run Here https://ideone.com/uDKGK
More Info http://graphics.stanford.edu/~seander/bithacks.html#CountBitsSetNaive
1st Brian Kernighan’s Algorithm:
Subtraction of 1 from a number toggles all the bits (from right to left) till the rightmost set bit(including the righmost set bit). So if we subtract a number by 1 and do bitwise & with itself (n & (n-1)), we unset the righmost set bit. If we do n & (n-1) in a loop and count the no of times loop executes we get the set bit count.
Beauty of the this solution is number of times it loops is equal to the number of set bits in a given integer.
1 Initialize count: = 0
2 If integer n is not zero
(a) Do bitwise & with (n-1) and assign the value back to n
n: = n&(n-1)
(b) Increment count by 1
(c) go to step 2
3 Else return count
#include
/* Function to get no of set bits in binary
representation of passed binary no. */
int countSetBits(int n)
{
unsigned int count = 0;
while (n)
{
n &= (n-1) ;
count++;
}
return count;
}
/* Program to test function countSetBits */
int main()
{
int i = 16;
printf("%d", countSetBits(i));
getchar();
return 0;
}
Time Complexity O(logn)
Space Complexity O(1)
Run Here https://ideone.com/2y2KJ
2nd Method is Most Efficient One !!!!!!
Assuming that the integer is 32 bits, this is pretty good:
x = (x & 0x55555555) + ((x >> 1) & 0x55555555);
x = (x & 0x33333333) + ((x >> 2) & 0x33333333);
x = (x & 0x0F0F0F0F) + ((x >> 4) & 0x0F0F0F0F);
x = (x & 0x00FF00FF) + ((x >> 8) & 0x00FF00FF);
x = (x & 0x0000FFFF) + ((x >> 16) & 0x0000FFFF);
where
0x55555555 = 01010101 01010101 01010101 01010101
0x33333333 = 00110011 00110011 00110011 00110011
0x0F0F0F0F = 00001111 00001111 00001111 00001111
0x00FF00FF = 00000000 11111111 00000000 11111111
0x0000FFFF = 00000000 00000000 11111111 11111111
Notice that the hex constants are respectively alternate bits,
alternate pairs of bits, alternate groups of four bits, alternate
bytes, and the low-order half of the int.
The first statement determines the number of one-bits in each pair of
bits. The second statement adds adjacent pairs of bits to get the
number of bits in each group of four bits. Then these are added to get
the number of bits in each byte, short int, and finally in the whole
int.
but it works at low level ??
Suppose that the first four bits of x from the left are abcd. Lets separate the bits into pairs with a comma: ab,cd. The first four bits of the hex constant0x55... are 0101, or separated into pairs: 01,01. The logical product of x with this constant is 0b,0d. The first four bits of x>>1 are 0abc, or separated into pairs are 0a,bc. The logical product of this with the constant is 0a,0c. The sum 0b,0d + 0a,0c is a+b,c+d, where a+b = 00, 01, or 10, and b+c = 00, 01, or 10. Thus we have replaced each pair of bits in x with the sum of the two bits originally in the pair.
The next statement uses the constant 0x333.... The first four bits of this are 0011, split into pairs as 00,11. The logical product of the first four bits of x with this constant gives 00,c+d. Furthermore (a+b,c+d)>>2 = 00,a+b. Then 00,c+d + 00,a+b gives the four-bit quantity a+b+c+d, i.e., the number of one bits set in the first four bits of the original x.
The next statements continue to double the number of bits included in each sum.
& so on
#include
using namespace std;
int main()
{
int x=0x00000016;
x = (x & 0x55555555) + ((x >> 1) & 0x55555555);
cout<
cout<
cout<
cout<
cout<
}
Time Complexity O(1)
Space Complexity O(1)
Run Here https://ideone.com/uDKGK
More Info http://graphics.stanford.edu/~seander/bithacks.html#CountBitsSetNaive
Labels:Data
D.E Shaw
,
DirectI Interview
,
Facebook Interview
,
Google Interview
,
Hyves Interview
,
Microsoft Interview
,
Yahoo Interview
Tuesday, May 3, 2011
WAP to Find Occurance of a Number N in Sorted Array in O(logn)
Given a sorted array and a number n.How can u find the number of occurance of n in the array . should be o(logn)
Modified Binary Search Algorithm
mid=low+high/2;
if(a[mid]>num)
search in right side & set low=mid+1 & return ;
else if(a[mid]
else //its important instead of just of printing the num or incrementing the counter //i tried if you will do like this then it will be O(n) not O(logn) , si i will add 1 to recursively call for left side + recursively call for right side so every time this line executes we are incrementing the counter &
return 1+left_binsearch()+right_binsearch thus it will be in O(logn)
you people can dry run for this 1 2 2 3 3 3 4 4 4 low=0 high=8 mid=4 & run it
#include
int CountFreq (int *A, int value, int low, int high)
{
int mid;
if (high < low)
return 0;
mid = low + (high - low);
if (A[mid] > value)
return CountFreq (A, value, low, mid - 1);
else if (A[mid] < value)
return CountFreq (A, value, mid + 1, high);
else
return 1 + CountFreq (A, value, low, mid - 1) + CountFreq (A, value, mid + 1, high);
}
int main() {
int A[] = { 1,2,2,2,2,3, 3, 3,4,4,4, 4};
int value = 2;
printf("%d\n", CountFreq(A, value, 0, sizeof(A)/sizeof(int)-1));
return 0;
}
TC O(n) consider ar[]={3,3,3,3,3,3}, & x=3 T(n)=2*T(n/2)+c leads to O(n)
Sc O(1)
Run Here https://ideone.com/clone/mTGes
Method 2 Modified Binary Search
1) Use Binary search to get index of the first occurrence of x in arr[]. Let the index of the first occurrence be i.
2) Use Binary search to get index of the last occurrence of x in arr[]. Let the index of the last occurrence be j.
3) Return (j – i + 1);
why it works because we know that array i sorted so if find the first occurrence at position i & last occurrence at position j then we are sure that all the elements between i & j are the same value what they at ith & jth position it works because array is sorted & we have done ....Cheers
#include
/* if x is present in arr[] then returns the index of FIRST occurrence
of x in arr[0..n-1], otherwise returns -1 */
int first(int arr[], int low, int high, int x, int n)
{
if(high >= low)
{
int mid = (low + high)/2; /*low + (high - low)/2;*/
if( ( mid == 0 || x > arr[mid-1]) && arr[mid] == x)
return mid;
else if(x > arr[mid])
return first(arr, (mid + 1), high, x, n);
else
return first(arr, low, (mid -1), x, n);
}
return -1;
}
/* if x is present in arr[] then returns the index of LAST occurrence
of x in arr[0..n-1], otherwise returns -1 */
int last(int arr[], int low, int high, int x, int n)
{
if(high >= low)
{
int mid = (low + high)/2; /*low + (high - low)/2;*/
if( ( mid == n-1 || x < arr[mid+1]) && arr[mid] == x )
return mid;
else if(x < arr[mid])
return last(arr, low, (mid -1), x, n);
else
return last(arr, (mid + 1), high, x, n);
}
return -1;
}
/* if x is present in arr[] then returns the count of occurrences of x,
otherwise returns -1. */
int count(int arr[], int x, int n)
{
int i; // index of first occurrence of x in arr[0..n-1]
int j; // index of last occurrence of x in arr[0..n-1]
/* get the index of first occurrence of x */
i = first(arr, 0, n-1, x, n);
/* If x doesn't exist in arr[] then return -1 */
if(i == -1)
return i;
/* Else get the index of last occurrence of x */
j = last(arr, 0, n-1, x, n);
/* return count */
return j-i+1;
}
/* driver program to test above functions */
int main()
{
int arr[] = {1, 2, 2, 2, 2, 3, 3};
int x = 2; // Element to be counted in arr[]
int n = sizeof(arr)/sizeof(arr[0]);
int c = count(arr, x, n);
printf(" %d occurs %d times ", x, c);
getchar();
return 0;
}
TC O(logn)
Sc O(1)
Run here https://ideone.com/J0enE
Modified Binary Search Algorithm
mid=low+high/2;
if(a[mid]>num)
search in right side & set low=mid+1 & return ;
else if(a[mid]
else //its important instead of just of printing the num or incrementing the counter //i tried if you will do like this then it will be O(n) not O(logn) , si i will add 1 to recursively call for left side + recursively call for right side so every time this line executes we are incrementing the counter &
return 1+left_binsearch()+right_binsearch thus it will be in O(logn)
you people can dry run for this 1 2 2 3 3 3 4 4 4 low=0 high=8 mid=4 & run it
#include
int CountFreq (int *A, int value, int low, int high)
{
int mid;
if (high < low)
return 0;
mid = low + (high - low);
if (A[mid] > value)
return CountFreq (A, value, low, mid - 1);
else if (A[mid] < value)
return CountFreq (A, value, mid + 1, high);
else
return 1 + CountFreq (A, value, low, mid - 1) + CountFreq (A, value, mid + 1, high);
}
int main() {
int A[] = { 1,2,2,2,2,3, 3, 3,4,4,4, 4};
int value = 2;
printf("%d\n", CountFreq(A, value, 0, sizeof(A)/sizeof(int)-1));
return 0;
}
TC O(n) consider ar[]={3,3,3,3,3,3}, & x=3 T(n)=2*T(n/2)+c leads to O(n)
Sc O(1)
Run Here https://ideone.com/clone/mTGes
Method 2 Modified Binary Search
1) Use Binary search to get index of the first occurrence of x in arr[]. Let the index of the first occurrence be i.
2) Use Binary search to get index of the last occurrence of x in arr[]. Let the index of the last occurrence be j.
3) Return (j – i + 1);
why it works because we know that array i sorted so if find the first occurrence at position i & last occurrence at position j then we are sure that all the elements between i & j are the same value what they at ith & jth position it works because array is sorted & we have done ....Cheers
#include
/* if x is present in arr[] then returns the index of FIRST occurrence
of x in arr[0..n-1], otherwise returns -1 */
int first(int arr[], int low, int high, int x, int n)
{
if(high >= low)
{
int mid = (low + high)/2; /*low + (high - low)/2;*/
if( ( mid == 0 || x > arr[mid-1]) && arr[mid] == x)
return mid;
else if(x > arr[mid])
return first(arr, (mid + 1), high, x, n);
else
return first(arr, low, (mid -1), x, n);
}
return -1;
}
/* if x is present in arr[] then returns the index of LAST occurrence
of x in arr[0..n-1], otherwise returns -1 */
int last(int arr[], int low, int high, int x, int n)
{
if(high >= low)
{
int mid = (low + high)/2; /*low + (high - low)/2;*/
if( ( mid == n-1 || x < arr[mid+1]) && arr[mid] == x )
return mid;
else if(x < arr[mid])
return last(arr, low, (mid -1), x, n);
else
return last(arr, (mid + 1), high, x, n);
}
return -1;
}
/* if x is present in arr[] then returns the count of occurrences of x,
otherwise returns -1. */
int count(int arr[], int x, int n)
{
int i; // index of first occurrence of x in arr[0..n-1]
int j; // index of last occurrence of x in arr[0..n-1]
/* get the index of first occurrence of x */
i = first(arr, 0, n-1, x, n);
/* If x doesn't exist in arr[] then return -1 */
if(i == -1)
return i;
/* Else get the index of last occurrence of x */
j = last(arr, 0, n-1, x, n);
/* return count */
return j-i+1;
}
/* driver program to test above functions */
int main()
{
int arr[] = {1, 2, 2, 2, 2, 3, 3};
int x = 2; // Element to be counted in arr[]
int n = sizeof(arr)/sizeof(arr[0]);
int c = count(arr, x, n);
printf(" %d occurs %d times ", x, c);
getchar();
return 0;
}
TC O(logn)
Sc O(1)
Run here https://ideone.com/J0enE
Labels:Data
Amazon Interview
,
Facebook Interview
,
Google Interview
,
Hyves Interview
Monday, May 2, 2011
WAP to Find Square root of Perfect Square Number Efficiently Yes in O(logn)
As its a perfect square!! So arrange numbers from 1 to n/2 and do a binary search..
ie for i from 1 to n/2
Now compare mind*mid to n
if mid*mid
else
recursively check left half
#include
int sqrtof_perfect(int start,int end,int n)
{
if(start>end)
return 0;
while(start<=end)
{
int mid=(start+end)/2;
//int temp=mid*mid;
if(mid*mid==n)
return mid;
else if(mid*mid>n)
end=mid-1;
else
start=mid+1;
}
return -1;
}
int main()
{
int n=144;//9;//25; // so
printf("\n %d",sqrtof_perfect(1,n/2,n));
getchar();
return 0;
}
TC O(logn)
Sc O(1)
ie for i from 1 to n/2
Now compare mind*mid to n
if mid*mid
else
recursively check left half
#include
int sqrtof_perfect(int start,int end,int n)
{
if(start>end)
return 0;
while(start<=end)
{
int mid=(start+end)/2;
//int temp=mid*mid;
if(mid*mid==n)
return mid;
else if(mid*mid>n)
end=mid-1;
else
start=mid+1;
}
return -1;
}
int main()
{
int n=144;//9;//25; // so
printf("\n %d",sqrtof_perfect(1,n/2,n));
getchar();
return 0;
}
TC O(logn)
Sc O(1)
Labels:Data
Amazon Interview
,
Facebook Interview
,
Google Interview
,
Hyves Interview
,
Microsoft Interview
Write a function that computes log2() using sqrt().
Well Its Very Interesting &n Tough Question Unless You Think ..Most of Us Stuck Whats The Use of Sqrt(0 to calculate log2() ..isn't it..?? i also stuck 1st but after doing some stuff with maths i was able to come up with this Algorithm so It Can be Done Using Simple Maths
As we Know
sqrt(x) = x^1/2
ln2(x) = ln(x) / ln(2)
ln2(sqrt(x)) = ln( x^(1/2) ) / ln(2)
= ((1/2) ln(x)) / ln(2)
= (1/2) * ln2(x)
So ln2(x) = 2 * ln2(sqrt(x))
class log_2
{
static double ln2;
static double epsilon = 0.0000001;
public static void main(String[] args)
{
ln2 = Math.log(2);
System.out.println("log2(10) = " + log2(10));
System.out.println("log2(10) = " + Math.log(10)/ln2);
}
public static double log2(double x)
{
if( x - 1 < epsilon ){
return (x-1)/ln2;
}
else{
return log2( Math.sqrt(x) ) * 2;
}
printf( " %d ", x/2);
}
}
Correctness Depends on epsilon value e.g no of places after decimal
Expected Output log2(10) = 3.3219282055116603
Actual Output log2(10) = 3.3219280948873626
Also You Know Taylor Series Extension of Log(1+x)= x - x^2/2 + x^3/3 + ... + ((-1)^(i+1).x^i)/i + o(x^(i+1))
More info http://en.wikipedia.org/wiki/Binary_logarithm
As we Know
sqrt(x) = x^1/2
ln2(x) = ln(x) / ln(2)
ln2(sqrt(x)) = ln( x^(1/2) ) / ln(2)
= ((1/2) ln(x)) / ln(2)
= (1/2) * ln2(x)
So ln2(x) = 2 * ln2(sqrt(x))
class log_2
{
static double ln2;
static double epsilon = 0.0000001;
public static void main(String[] args)
{
ln2 = Math.log(2);
System.out.println("log2(10) = " + log2(10));
System.out.println("log2(10) = " + Math.log(10)/ln2);
}
public static double log2(double x)
{
if( x - 1 < epsilon ){
return (x-1)/ln2;
}
else{
return log2( Math.sqrt(x) ) * 2;
}
printf( " %d ", x/2);
}
}
Correctness Depends on epsilon value e.g no of places after decimal
Expected Output log2(10) = 3.3219282055116603
Actual Output log2(10) = 3.3219280948873626
Also You Know Taylor Series Extension of Log(1+x)= x - x^2/2 + x^3/3 + ... + ((-1)^(i+1).x^i)/i + o(x^(i+1))
More info http://en.wikipedia.org/wiki/Binary_logarithm
Labels:Data
Adobe Question
,
Amazon Interview
,
Facebook Interview
,
Google Interview
,
Hyves Interview
Saturday, April 30, 2011
How to find if a node/pointer corrupted in a linked list
How would you find out if one of the pointers in a linked list is corrupted or not?
This is a really good interview question. The reason is that linked lists are used in a wide variety of scenarios and being able to detect and correct pointer corruptions might be a very valuable tool. For example, data blocks associated with files in a file system are usually stored as linked lists. Each data block points to the next data block. A single corrupt pointer can cause the entire file to be lost!
1 Discover & Fix Bugs
Discover and fix bugs when they corrupt the linked list and not when effect becomes visible in some other part of the program. Perform frequent consistency checks (to see if the linked list is indeed holding the data that you inserted into it).
2 set Pointer to NUll after Freeing Object
It is good programming practice to set the pointer value to NULL immediately after freeing the memory pointed at by the pointer. This will help in debugging, because it will tell you that the object was freed somewhere beforehand. Keep track of how many objects are pointing to a object using reference counts if required.
3 Use Debugger Tool Like DDD,Purify,
Use a good debugger to see how the datastructures are getting corrupted and trace down the problem. Debuggers like ddd on linux and memory profilers like Purify, Electric fence are good starting points. These tools should help you track down heap corruption issues easily.
4.Avoid Global Variable
Avoid global variables when traversing and manipulating linked lists. Imagine what would happen if a function which is only supposed to traverse a linked list using a global head pointer accidently sets the head pointer to NULL!.
5 Check Add& Delete Node After such Opeartion
Its a good idea to check the addNode() and the deleteNode() routines and test them for all types of scenarios. This should include tests for inserting/deleting nodes at the front/middle/end of the linked list, working with an empty linked list, running out of memory when using malloc() when allocating memory for new nodes, writing through NULL pointers, writing more data into the node fields then they can hold (resulting in corrupting the (probably adjacent) “prev” and “next” pointer fields), make sure bug fixes and enhancements to the linked list code are reviewed and well tested (a lot of bugs come from quick and dirty bug fixing), log and handle all possible errors (this will help you a lot while debugging), add multiple levels of logging so that you can dig through the logs. The list is endless…
6.Keep Track of Number of Nodes After Every Node after Initializing Linked List
Each node can have an extra field associated with it. This field indicates the number of nodes after this node in the linked list. This extra field needs to be kept up-to-date when we inserte or delete nodes in the linked list (It might become slightly complicated when insertion or deletion happens not at end, but anywhere in the linked list). Then, if for any node, p->field > 0 and p->next == NULL, it surely points to a pointer corruption.
You could also keep the count of the total number of nodes in a linked list and use it to check if the list is indeed having those many nodes or not.
The problem in detecting such pointer corruptions in C is that its only the programmer who knows that the pointer is corrupted. The program has no way of knowing that something is wrong. So the best way to fix these errors is check your logic and test your code to the maximum possible extent. I am not aware of ways in C to recover the lost nodes of a corrupted linked list. C does not track pointers so there is no good way to know if an arbitrary pointer has been corrupted or not. The platform may have a library service that checks if a pointer points to valid memory (for instance on Win32 there is a IsBadReadPtr, IsBadWritePtr API.) If you detect a cycle in the link list, it’s definitely bad. If it’s a doubly linked list you can verify, pNode->Next->Prev == pNode.
I have a hunch that interviewers who ask this question are probably hinting at something called Smart Pointers in C++. Smart pointers are particularly useful in the face of exceptions as they ensure proper destruction of dynamically allocated objects. They can also be used to keep track of dynamically allocated objects shared by multiple owners. This topic is out of scope here, but you can find lots of material on the Internet for Smart Pointers.
This is a really good interview question. The reason is that linked lists are used in a wide variety of scenarios and being able to detect and correct pointer corruptions might be a very valuable tool. For example, data blocks associated with files in a file system are usually stored as linked lists. Each data block points to the next data block. A single corrupt pointer can cause the entire file to be lost!
1 Discover & Fix Bugs
Discover and fix bugs when they corrupt the linked list and not when effect becomes visible in some other part of the program. Perform frequent consistency checks (to see if the linked list is indeed holding the data that you inserted into it).
2 set Pointer to NUll after Freeing Object
It is good programming practice to set the pointer value to NULL immediately after freeing the memory pointed at by the pointer. This will help in debugging, because it will tell you that the object was freed somewhere beforehand. Keep track of how many objects are pointing to a object using reference counts if required.
3 Use Debugger Tool Like DDD,Purify,
Use a good debugger to see how the datastructures are getting corrupted and trace down the problem. Debuggers like ddd on linux and memory profilers like Purify, Electric fence are good starting points. These tools should help you track down heap corruption issues easily.
4.Avoid Global Variable
Avoid global variables when traversing and manipulating linked lists. Imagine what would happen if a function which is only supposed to traverse a linked list using a global head pointer accidently sets the head pointer to NULL!.
5 Check Add& Delete Node After such Opeartion
Its a good idea to check the addNode() and the deleteNode() routines and test them for all types of scenarios. This should include tests for inserting/deleting nodes at the front/middle/end of the linked list, working with an empty linked list, running out of memory when using malloc() when allocating memory for new nodes, writing through NULL pointers, writing more data into the node fields then they can hold (resulting in corrupting the (probably adjacent) “prev” and “next” pointer fields), make sure bug fixes and enhancements to the linked list code are reviewed and well tested (a lot of bugs come from quick and dirty bug fixing), log and handle all possible errors (this will help you a lot while debugging), add multiple levels of logging so that you can dig through the logs. The list is endless…
6.Keep Track of Number of Nodes After Every Node after Initializing Linked List
Each node can have an extra field associated with it. This field indicates the number of nodes after this node in the linked list. This extra field needs to be kept up-to-date when we inserte or delete nodes in the linked list (It might become slightly complicated when insertion or deletion happens not at end, but anywhere in the linked list). Then, if for any node, p->field > 0 and p->next == NULL, it surely points to a pointer corruption.
You could also keep the count of the total number of nodes in a linked list and use it to check if the list is indeed having those many nodes or not.
The problem in detecting such pointer corruptions in C is that its only the programmer who knows that the pointer is corrupted. The program has no way of knowing that something is wrong. So the best way to fix these errors is check your logic and test your code to the maximum possible extent. I am not aware of ways in C to recover the lost nodes of a corrupted linked list. C does not track pointers so there is no good way to know if an arbitrary pointer has been corrupted or not. The platform may have a library service that checks if a pointer points to valid memory (for instance on Win32 there is a IsBadReadPtr, IsBadWritePtr API.) If you detect a cycle in the link list, it’s definitely bad. If it’s a doubly linked list you can verify, pNode->Next->Prev == pNode.
I have a hunch that interviewers who ask this question are probably hinting at something called Smart Pointers in C++. Smart pointers are particularly useful in the face of exceptions as they ensure proper destruction of dynamically allocated objects. They can also be used to keep track of dynamically allocated objects shared by multiple owners. This topic is out of scope here, but you can find lots of material on the Internet for Smart Pointers.
Labels:Data
Amazon Interview
,
D.E Shaw
,
DirectI Interview
,
Facebook Interview
,
FlipKart Interview
,
Google Interview
,
Hyves Interview
,
Microsoft Interview
,
Yahoo Interview
Friday, April 29, 2011
WAP to Check if if two strings are anagrams or not. in O(n) ..?
There are 4 ways to solve this problem: as i can solve it each has complexity Issue
Solution #1: Sort the strings
boolean anagram(String s, String t)
{
return sort(s) == sort(t);
}
# include
# include
# include
/* FOLLOWING FUNCTIONS ARE ONLY FOR SORTING
PURPOSE */
void exchange(char *a, char *b)
{
char temp;
temp = *a;
*a = *b;
*b = temp;
}
int partition(char A[], int si, int ei)
{
char x = A[ei];
int i = (si - 1);
int j;
for (j = si; j <= ei - 1; j++)
{
if(A[j] <= x)
{
i++;
exchange(&A[i], &A[j]);
}
}
exchange (&A[i + 1], &A[ei]);
return (i + 1);
}
/* Implementation of Quick Sort
A[] --> Array to be sorted
si --> Starting index
ei --> Ending index
*/
void quickSort(char A[], int si, int ei)
{
int pi; /* Partitioning index */
if(si < ei)
{
pi = partition(A, si, ei);
quickSort(A, si, pi - 1);
quickSort(A, pi + 1, ei);
}
}
int anagram(char* a,int a_len,char* b,int b_len)
{
quickSort(a,0,a_len);
quickSort(b,0,b_len);
return (strcmp(a,b));
}
/* Driver program to test removeDups */
int main()
{
char a[] = "madonna louise ciccone";
char b[] ="occasional nude income";
int n=sizeof(a)/sizeof(char);
int m=sizeof(b)/sizeof(char);
printf( " %d ", anagram(a,n,b,m));
getchar();
return 0;
}
TC O(nlogn)
SC O(1)
Run here https://ideone.com/swXVj
solution #2:
Check if the two strings have identical counts for each unique char.
class Anagram
{
public static void main(String a[])
{
System.out.println(anagram(new String("william shakespeare"), new String("iam aweakishspeller")));
}
public static boolean anagram(String s, String t)
{
if (s.length() != t.length()) return false;
int[] letters = new int[256];
int num_unique_chars = 0;
int num_completed_t = 0;
char[] s_array = s.toCharArray();
for (char c : s_array) { // count number of each char in s.
if (letters[c] == 0) ++num_unique_chars;
++letters[c];
}
for (int i = 0; i < t.length(); ++i) {
int c = (int) t.charAt(i);
if (letters[c] == 0) { // Found more of char c in t than in s.
return false;
}
--letters[c];
if (letters[c] == 0) {
++num_completed_t;
if (num_completed_t == num_unique_chars) {
// it’s a match if t has been processed completely
return i == t.length() - 1;
}
}
}
return false;
}
}
TC o(n)
Scv o(n)
Run here https://ideone.com/mpWTO
3rd & 4th Solution
Take XOR of both the strings ..if they are anagram then result will be zero.
Its has two way to solve & cool ,Most Efficient as I can Say to solve the problem
#include
#include
using namespace std;
int isAnagram(char* a, char* b, int len)
{
int zor = 0;
for(int i = 0; i < len; ++i)
{
zor ^= a[i] - '0';
//printf( "%d %d \t ", (a[i]-'0'),zor);
zor ^= b[i] - '0';
//printf( "%d %d \n ", (b[i]-'0'),zor);
}
if(zor == 0)
return 1;
return 0;
}
4th Solution
Check for both xor & sum of each string if xor=0 & both sum are equals then string are Anagram of each other
int check_anagram(const char* str1, const char* str2)
{
int len = strlen(str1);
int l2=strlen(str2);
if(len != l2)
return 0;
int xorval=0;
int sum1=0,sum2=0;
for(int i=0;i
sum1 += str1[i];
sum2 += str2[i];
xorval ^= str1[i] ^ str2[i];
}
if((xorval == 0 && (sum1 == sum2))==true)
return 1;
else return 0;
return 0;
}
int main()
{
char a[] = "madonna louise ciccone";
//"william shakespeare";//"abcd";
char b[] ="occasional nude income";
//"iam aweakishspeller";//"badc";
int n=sizeof(a)/sizeof(char);//if both anagram size should be same so no issue here
printf( " %d %d ",isAnagram(a, b, n),check_anagram(a,b));
return 0;
}
TC O(n)
Sc (1)
Run Here https://ideone.com/UDk5G
Solution #1: Sort the strings
boolean anagram(String s, String t)
{
return sort(s) == sort(t);
}
# include
# include
# include
/* FOLLOWING FUNCTIONS ARE ONLY FOR SORTING
PURPOSE */
void exchange(char *a, char *b)
{
char temp;
temp = *a;
*a = *b;
*b = temp;
}
int partition(char A[], int si, int ei)
{
char x = A[ei];
int i = (si - 1);
int j;
for (j = si; j <= ei - 1; j++)
{
if(A[j] <= x)
{
i++;
exchange(&A[i], &A[j]);
}
}
exchange (&A[i + 1], &A[ei]);
return (i + 1);
}
/* Implementation of Quick Sort
A[] --> Array to be sorted
si --> Starting index
ei --> Ending index
*/
void quickSort(char A[], int si, int ei)
{
int pi; /* Partitioning index */
if(si < ei)
{
pi = partition(A, si, ei);
quickSort(A, si, pi - 1);
quickSort(A, pi + 1, ei);
}
}
int anagram(char* a,int a_len,char* b,int b_len)
{
quickSort(a,0,a_len);
quickSort(b,0,b_len);
return (strcmp(a,b));
}
/* Driver program to test removeDups */
int main()
{
char a[] = "madonna louise ciccone";
char b[] ="occasional nude income";
int n=sizeof(a)/sizeof(char);
int m=sizeof(b)/sizeof(char);
printf( " %d ", anagram(a,n,b,m));
getchar();
return 0;
}
TC O(nlogn)
SC O(1)
Run here https://ideone.com/swXVj
solution #2:
Check if the two strings have identical counts for each unique char.
class Anagram
{
public static void main(String a[])
{
System.out.println(anagram(new String("william shakespeare"), new String("iam aweakishspeller")));
}
public static boolean anagram(String s, String t)
{
if (s.length() != t.length()) return false;
int[] letters = new int[256];
int num_unique_chars = 0;
int num_completed_t = 0;
char[] s_array = s.toCharArray();
for (char c : s_array) { // count number of each char in s.
if (letters[c] == 0) ++num_unique_chars;
++letters[c];
}
for (int i = 0; i < t.length(); ++i) {
int c = (int) t.charAt(i);
if (letters[c] == 0) { // Found more of char c in t than in s.
return false;
}
--letters[c];
if (letters[c] == 0) {
++num_completed_t;
if (num_completed_t == num_unique_chars) {
// it’s a match if t has been processed completely
return i == t.length() - 1;
}
}
}
return false;
}
}
TC o(n)
Scv o(n)
Run here https://ideone.com/mpWTO
3rd & 4th Solution
Take XOR of both the strings ..if they are anagram then result will be zero.
Its has two way to solve & cool ,Most Efficient as I can Say to solve the problem
#include
#include
using namespace std;
int isAnagram(char* a, char* b, int len)
{
int zor = 0;
for(int i = 0; i < len; ++i)
{
zor ^= a[i] - '0';
//printf( "%d %d \t ", (a[i]-'0'),zor);
zor ^= b[i] - '0';
//printf( "%d %d \n ", (b[i]-'0'),zor);
}
if(zor == 0)
return 1;
return 0;
}
4th Solution
Check for both xor & sum of each string if xor=0 & both sum are equals then string are Anagram of each other
int check_anagram(const char* str1, const char* str2)
{
int len = strlen(str1);
int l2=strlen(str2);
if(len != l2)
return 0;
int xorval=0;
int sum1=0,sum2=0;
for(int i=0;i
sum1 += str1[i];
sum2 += str2[i];
xorval ^= str1[i] ^ str2[i];
}
if((xorval == 0 && (sum1 == sum2))==true)
return 1;
else return 0;
return 0;
}
int main()
{
char a[] = "madonna louise ciccone";
//"william shakespeare";//"abcd";
char b[] ="occasional nude income";
//"iam aweakishspeller";//"badc";
int n=sizeof(a)/sizeof(char);//if both anagram size should be same so no issue here
printf( " %d %d ",isAnagram(a, b, n),check_anagram(a,b));
return 0;
}
TC O(n)
Sc (1)
Run Here https://ideone.com/UDk5G
Labels:Data
Amazon Interview
,
Facebook Interview
,
Google Interview
,
Hyves Interview
Saturday, April 23, 2011
WAP to print 2D array matrix in Spiral Order
Question: Given a 2D array / matrix of integers. Write a program to print the elements in spiral order. Consider a matrix as show in the diagram to the right. The desired output of the program should be as: 1,2,3,4,8,12,16,20,19,18,17,13,9,5,6, 7,11,15,14,10.

Solution: There are several ways to solve this problem, but I am mentioning a method that is intuitive to understand and easy to implement. The idea is to consider the matrix similar to onion which can be peeled layer after layer. We can use the same approach to print the outer layer of the matrix and keep doing it recursively on a smaller matrix (with 1 less row and 1 less column).
Refer to the image below for a visual explanation. We start by printing the top-right layer of the matrix by calling the print_layer_top_right. It will print 1,2,3,4,8,12,16,20. The print_layer_top_right method then calls the print_layer_bottom_left method which will print 19,18,17,13,9,5. If you observe the size of the target matrix is reducing after each call. Each method basically calls the other method and passes the matrix indexes for the reduced matrix. Both methods take 4 index parameters which represent the target matrix. When the target matrix size is such that there is only one layer left the recursion terminates and by this time the code has printed all the numbers in the full matrix.
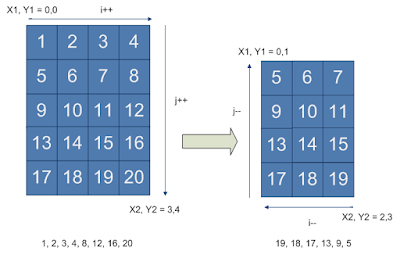
Code (C language):
#include
void print_layer_top_right(int a[][4], int x1, int y1, int x2, int y2);
void print_layer_bottom_left(int a[][4], int x1, int y1, int x2, int y2);
int main(void)
{
int a[5][4] = {
{1,2,3,4},
{5,6,7,8},
{9,10,11,12},
{13,14,15,16},
{17,18,19,20}
};
print_layer_top_right(a,0,0,3,4);
}
//
// prints the top and right shells of the matrix
//
void print_layer_top_right(int a[][4], int x1, int y1, int x2, int y2)
{
int i = 0, j = 0;
// print the row
for(i = x1; i<=x2; i++)
{
printf("%d,", a[y1][i]);
}
//print the column
for(j = y1 + 1; j <= y2; j++)
{
printf("%d,", a[j][x2]);
}
// see if we have more cells left
if(x2-x1 > 0)
{
// 'recursively' call the function to print the bottom-left layer
print_layer_bottom_left(a, x1, y1 + 1, x2-1, y2);
}
}
//
// prints the bottom and left shells of the matrix
//
void print_layer_bottom_left(int a[][4], int x1, int y1, int x2, int y2)
{
int i = 0, j = 0;
//print the row of the matrix in reverse
for(i = x2; i>=x1; i--)
{
printf("%d,", a[y2][i]);
}
// print the last column of the matrix in reverse
for(j = y2 - 1; j >= y1; j--)
{
printf("%d,", a[j][x1]);
}
if(x2-x1 > 0)
{
// 'recursively' call the function to print the top-right layer
print_layer_top_right(a, x1+1, y1, x2, y2-1);
}
}

Solution: There are several ways to solve this problem, but I am mentioning a method that is intuitive to understand and easy to implement. The idea is to consider the matrix similar to onion which can be peeled layer after layer. We can use the same approach to print the outer layer of the matrix and keep doing it recursively on a smaller matrix (with 1 less row and 1 less column).
Refer to the image below for a visual explanation. We start by printing the top-right layer of the matrix by calling the print_layer_top_right. It will print 1,2,3,4,8,12,16,20. The print_layer_top_right method then calls the print_layer_bottom_left method which will print 19,18,17,13,9,5. If you observe the size of the target matrix is reducing after each call. Each method basically calls the other method and passes the matrix indexes for the reduced matrix. Both methods take 4 index parameters which represent the target matrix. When the target matrix size is such that there is only one layer left the recursion terminates and by this time the code has printed all the numbers in the full matrix.

Code (C language):
<script type="syntaxhighlighter" class="brush: html"><![CDATA[
#include
void print_layer_top_right(int a[][4], int x1, int y1, int x2, int y2);
void print_layer_bottom_left(int a[][4], int x1, int y1, int x2, int y2);
int main(void)
{
int a[5][4] = {
{1,2,3,4},
{5,6,7,8},
{9,10,11,12},
{13,14,15,16},
{17,18,19,20}
};
print_layer_top_right(a,0,0,3,4);
}
//
// prints the top and right shells of the matrix
//
void print_layer_top_right(int a[][4], int x1, int y1, int x2, int y2)
{
int i = 0, j = 0;
// print the row
for(i = x1; i<=x2; i++)
{
printf("%d,", a[y1][i]);
}
//print the column
for(j = y1 + 1; j <= y2; j++)
{
printf("%d,", a[j][x2]);
}
// see if we have more cells left
if(x2-x1 > 0)
{
// 'recursively' call the function to print the bottom-left layer
print_layer_bottom_left(a, x1, y1 + 1, x2-1, y2);
}
}
//
// prints the bottom and left shells of the matrix
//
void print_layer_bottom_left(int a[][4], int x1, int y1, int x2, int y2)
{
int i = 0, j = 0;
//print the row of the matrix in reverse
for(i = x2; i>=x1; i--)
{
printf("%d,", a[y2][i]);
}
// print the last column of the matrix in reverse
for(j = y2 - 1; j >= y1; j--)
{
printf("%d,", a[j][x1]);
}
if(x2-x1 > 0)
{
// 'recursively' call the function to print the top-right layer
print_layer_top_right(a, x1+1, y1, x2, y2-1);
}
}
]]></script>
Run Here https://ideone.com/ut0Hx
Friday, April 22, 2011
WAP to Write Find MaximumSize Sub-Matrix From Given Matrxi having Size of R*C
Maximum size square sub-matrix with all 1s
April 4, 2010
Given a binary matrix, find out the maximum size square sub-matrix with all 1s.
For example, consider the below binary matrix.
0 1 1 0 1
1 1 0 1 0
0 1 1 1 0
1 1 1 1 0
1 1 1 1 1
0 0 0 0 0
The maximum square sub-matrix with all set bits is
1 1 1
1 1 1
1 1 1
Algorithm:
Let the given binary matrix be M[R][C]. The idea of the algorithm is to construct an auxiliary size matrix S[][] in which each entry S[i][j] represents size of the square sub-matrix with all 1s including M[i][j] and M[i][j] is the rightmost and bottommost entry in sub-matrix.
1) Construct a sum matrix S[R][C] for the given M[R][C].
a) Copy first row and first columns as it is from M[][] to S[][]
b) For other entries, use following expressions to construct S[][]
If M[i][j] is 1 then
S[i][j] = min(S[i][j-1], S[i-1][j], S[i-1][j-1]) + 1
Else /*If M[i][j] is 0*/
S[i][j] = 0
2) Find the maximum entry in S[R][C]
3) Using the value and coordinates of maximum entry in S[i], print
sub-matrix of M[][]
For the given M[R][C] in above example, constructed S[R][C] would be:
0 1 1 0 1
1 1 0 1 0
0 1 1 1 0
1 1 2 2 0
1 2 2 3 1
0 0 0 0 0
The value of maximum entry in above matrix is 3 and coordinates of the entry are (4, 3). Using the maximum value and its coordinates, we can find out the required sub-matrix.
C program
#include
#define bool int
#define R 6
#define C 5
/* UTILITY FUNCTIONS */
/* Function to get minimum of three values */
int min(int a, int b, int c)
{
int m = a;
if (m > b)
m = b;
if (m > c)
m = c;
return m;
}
void printMaxSubSquare(bool M[R][C])
{
int i,j;
int S[R][C];
int max_of_s, max_i, max_j;
/* Set first column of S[][]*/
for(i = 0; i < R; i++)
S[i][0] = M[i][0];
/* Set first row of S[][]*/
for(j = 0; j < C; j++)
S[0][j] = M[0][j];
/* Construct other entries of S[][]*/
for(i = 1; i < R; i++)
{
for(j = 1; j < C; j++)
{
if(M[i][j] == 1)
S[i][j] = min(S[i][j-1], S[i-1][j], S[i-1][j-1]) + 1;
else
S[i][j] = 0;
}
}
/* Find the maximum entry, and indexes of maximum entry
in S[][] */
max_of_s = S[0][0]; max_i = 0; max_j = 0;
for(i = 0; i < R; i++)
{
for(j = 0; j < C; j++)
{
if(max_of_s < S[i][j])
{
max_of_s = S[i][j];
max_i = i;
max_j = j;
}
}
}
printf("\n Maximum size sub-matrix is: \n");
for(i = max_i; i > max_i - max_of_s; i--)
{
for(j = max_j; j > max_j - max_of_s; j--)
{
printf("%d ", M[i][j]);
}
printf("\n");
}
}
/* Driver function to test above functions */
int main()
{
bool M[R][C] = {{0, 1, 1, 0, 1},
{1, 1, 0, 1, 0},
{0, 1, 1, 1, 0},
{1, 1, 1, 1, 0},
{1, 1, 1, 1, 1},
{0, 0, 0, 0, 0}};
printMaxSubSquare(M);
getchar();
}
Run Here https://ideone.com/oFXO6
April 4, 2010
Given a binary matrix, find out the maximum size square sub-matrix with all 1s.
For example, consider the below binary matrix.
0 1 1 0 1
1 1 0 1 0
0 1 1 1 0
1 1 1 1 0
1 1 1 1 1
0 0 0 0 0
The maximum square sub-matrix with all set bits is
1 1 1
1 1 1
1 1 1
Algorithm:
Let the given binary matrix be M[R][C]. The idea of the algorithm is to construct an auxiliary size matrix S[][] in which each entry S[i][j] represents size of the square sub-matrix with all 1s including M[i][j] and M[i][j] is the rightmost and bottommost entry in sub-matrix.
1) Construct a sum matrix S[R][C] for the given M[R][C].
a) Copy first row and first columns as it is from M[][] to S[][]
b) For other entries, use following expressions to construct S[][]
If M[i][j] is 1 then
S[i][j] = min(S[i][j-1], S[i-1][j], S[i-1][j-1]) + 1
Else /*If M[i][j] is 0*/
S[i][j] = 0
2) Find the maximum entry in S[R][C]
3) Using the value and coordinates of maximum entry in S[i], print
sub-matrix of M[][]
For the given M[R][C] in above example, constructed S[R][C] would be:
0 1 1 0 1
1 1 0 1 0
0 1 1 1 0
1 1 2 2 0
1 2 2 3 1
0 0 0 0 0
The value of maximum entry in above matrix is 3 and coordinates of the entry are (4, 3). Using the maximum value and its coordinates, we can find out the required sub-matrix.
C program
#include
#define bool int
#define R 6
#define C 5
/* UTILITY FUNCTIONS */
/* Function to get minimum of three values */
int min(int a, int b, int c)
{
int m = a;
if (m > b)
m = b;
if (m > c)
m = c;
return m;
}
void printMaxSubSquare(bool M[R][C])
{
int i,j;
int S[R][C];
int max_of_s, max_i, max_j;
/* Set first column of S[][]*/
for(i = 0; i < R; i++)
S[i][0] = M[i][0];
/* Set first row of S[][]*/
for(j = 0; j < C; j++)
S[0][j] = M[0][j];
/* Construct other entries of S[][]*/
for(i = 1; i < R; i++)
{
for(j = 1; j < C; j++)
{
if(M[i][j] == 1)
S[i][j] = min(S[i][j-1], S[i-1][j], S[i-1][j-1]) + 1;
else
S[i][j] = 0;
}
}
/* Find the maximum entry, and indexes of maximum entry
in S[][] */
max_of_s = S[0][0]; max_i = 0; max_j = 0;
for(i = 0; i < R; i++)
{
for(j = 0; j < C; j++)
{
if(max_of_s < S[i][j])
{
max_of_s = S[i][j];
max_i = i;
max_j = j;
}
}
}
printf("\n Maximum size sub-matrix is: \n");
for(i = max_i; i > max_i - max_of_s; i--)
{
for(j = max_j; j > max_j - max_of_s; j--)
{
printf("%d ", M[i][j]);
}
printf("\n");
}
}
/* Driver function to test above functions */
int main()
{
bool M[R][C] = {{0, 1, 1, 0, 1},
{1, 1, 0, 1, 0},
{0, 1, 1, 1, 0},
{1, 1, 1, 1, 0},
{1, 1, 1, 1, 1},
{0, 0, 0, 0, 0}};
printMaxSubSquare(M);
getchar();
}
Run Here https://ideone.com/oFXO6
Wednesday, April 6, 2011
WAP to Generate Unique Combination from Given Set ot String
What is combination and how is it different from a permutation?
The mathematics' gurus would know this by heart, but I am going to refer to the Wikipedia for a proper definition.
"A combination is an un-ordered collection of unique sizes. (An ordered collection is called a permutation.)" from the Wikipedia article.
For example,
For a given String "ABCD",
a combination of un-ordered collection of unique sizes will be
[ABCD, BCD, ABD, ABC, ACD, AC, AD, AB, BC, BD, CD, D, A, B, C]
From my quick Google search, I also found out
"Number of ways of selecting zero or more things from ‘n’ different things is given by:- ( 2 ^ n - 1 ) "(from this article).
If we apply this formula in the above example, String "ABCD" with length of 4 should have ( 2 * 2 * 2 * 2 ) - 1 = 15 combinations.
This is exaclty what we are going to acheive in our code - Finding all possible combinations of characters from a given String. Note that for simplicity, we are going to assume that the input String (whose different combinations are going to be found) would not have any repetitive characters in it.
What is recursive programming?
Lets get a formal definition from Wikipedia:
"Creating a recursive procedure essentially requires defining a "base case", and then defining rules to break down more complex cases into the base case. Key to a recursive procedure is that with each recursive call, the problem domain must be reduced in such a way that eventually the base case is arrived at."
In very simple terms, a method calling itself again and again until a particular condition is met is called recursive programming.
Implementation:
The algorithm discussed below to solve this problem is chosen for its simplicity and ease of understanding. It may not be the most effective algorithm but it definitely solves this particular problem and is extremely simple.
Some points to note about this problem.
1. The given String itself is one of the combinations. For example, one of the combinations of the String "ABCD" is "ABCD" itself.
2. Every character in the String will be a combination. For example, for the String "ABCD" -- > "A", "B", "C", "D" will be some of the combinations.
Algorithm
To find the combinations of a String:
Step 1: Add the String to the combination results.
Step 2: If the String has just one character in it,
then stop the current line of execution.
Step 3: Create new sub-words from the String by removing one letter at a time.
If the String is "ABCD", form sub-words like "BCD", "ACD", "ABD", "ABC"
Step 4: For each of the sub-word, go to Step 1
import java.io.IOException;
import java.util.HashSet;
import java.util.Scanner;
import java.util.Set;
class StringCombinations
{
private Set combinations = new HashSet();
public StringCombinations(String sInputString)
{
generate(sInputString);
System.out.println("*** Generated " + combinations .size() + " combinations ***");
System.out.println(combinations);
}
public void generate(String word)
{
// Add this word to our combination results set
// System.out.println(word);
combinations.add(word);
// If the word has only one character we break the
// recursion
if (word.length() == 1)
{
combinations.add(word);
return;
}
// Go through every position of the word
for (int i = 0; i < word.length(); i++)
{
// Remove the character at the current position
// all call this method with that String (Recursion!)
generate(word.substring(0,i) + word.substring(i+1));
}
}
public static String readCommandLineInput(String inputMessage)
{
String inputLine ="abcd";
return inputLine;
}
public static void main(String args[])
{
// Request and read user input
String sInstruction = "Enter a String: \n";
String sInputString = readCommandLineInput(sInstruction);
new StringCombinations(sInputString);
}
}// End of StringCombinations
Run Here https://ideone.com/EPV9i
Another Informative Link http://www.codeguru.com/cpp/cpp/algorithms/combinations/article.php/c5117
The mathematics' gurus would know this by heart, but I am going to refer to the Wikipedia for a proper definition.
"A combination is an un-ordered collection of unique sizes. (An ordered collection is called a permutation.)" from the Wikipedia article.
For example,
For a given String "ABCD",
a combination of un-ordered collection of unique sizes will be
[ABCD, BCD, ABD, ABC, ACD, AC, AD, AB, BC, BD, CD, D, A, B, C]
From my quick Google search, I also found out
"Number of ways of selecting zero or more things from ‘n’ different things is given by:- ( 2 ^ n - 1 ) "(from this article).
If we apply this formula in the above example, String "ABCD" with length of 4 should have ( 2 * 2 * 2 * 2 ) - 1 = 15 combinations.
This is exaclty what we are going to acheive in our code - Finding all possible combinations of characters from a given String. Note that for simplicity, we are going to assume that the input String (whose different combinations are going to be found) would not have any repetitive characters in it.
What is recursive programming?
Lets get a formal definition from Wikipedia:
"Creating a recursive procedure essentially requires defining a "base case", and then defining rules to break down more complex cases into the base case. Key to a recursive procedure is that with each recursive call, the problem domain must be reduced in such a way that eventually the base case is arrived at."
In very simple terms, a method calling itself again and again until a particular condition is met is called recursive programming.
Implementation:
The algorithm discussed below to solve this problem is chosen for its simplicity and ease of understanding. It may not be the most effective algorithm but it definitely solves this particular problem and is extremely simple.
Some points to note about this problem.
1. The given String itself is one of the combinations. For example, one of the combinations of the String "ABCD" is "ABCD" itself.
2. Every character in the String will be a combination. For example, for the String "ABCD" -- > "A", "B", "C", "D" will be some of the combinations.
Algorithm
To find the combinations of a String:
Step 1: Add the String to the combination results.
Step 2: If the String has just one character in it,
then stop the current line of execution.
Step 3: Create new sub-words from the String by removing one letter at a time.
If the String is "ABCD", form sub-words like "BCD", "ACD", "ABD", "ABC"
Step 4: For each of the sub-word, go to Step 1
import java.io.IOException;
import java.util.HashSet;
import java.util.Scanner;
import java.util.Set;
class StringCombinations
{
private Set combinations = new HashSet();
public StringCombinations(String sInputString)
{
generate(sInputString);
System.out.println("*** Generated " + combinations .size() + " combinations ***");
System.out.println(combinations);
}
public void generate(String word)
{
// Add this word to our combination results set
// System.out.println(word);
combinations.add(word);
// If the word has only one character we break the
// recursion
if (word.length() == 1)
{
combinations.add(word);
return;
}
// Go through every position of the word
for (int i = 0; i < word.length(); i++)
{
// Remove the character at the current position
// all call this method with that String (Recursion!)
generate(word.substring(0,i) + word.substring(i+1));
}
}
public static String readCommandLineInput(String inputMessage)
{
String inputLine ="abcd";
return inputLine;
}
public static void main(String args[])
{
// Request and read user input
String sInstruction = "Enter a String: \n";
String sInputString = readCommandLineInput(sInstruction);
new StringCombinations(sInputString);
}
}// End of StringCombinations
Run Here https://ideone.com/EPV9i
Another Informative Link http://www.codeguru.com/cpp/cpp/algorithms/combinations/article.php/c5117
Sunday, April 3, 2011
Dominator of an array ...Majority Element In Different Way
Majority Element Different Possible Solutions
Solution 1: A basic solution is to scan entire array for checking for every element in the array. If any element occurs more than n/2 time, prints it and break the loop. This will be of O(n^2) complexity.
Solution 2: Sort the entire array in O(nlogn) and then in one pass keep counting the elements. This will be of O(nlogn) + O() = O(nlogn) complexity. #try it
Solution 3 Using BitCount Array
#include
int findmaj(int arr[], int n)
{
int bitcount[32];
int i, j, x;
for(i = 0; i < 32; i++)
bitcount[i] = 0;
for (i = 0; i < n; i++)
for (j = 0; j < 32; j++)
if (arr[i] & (1 << j)) // if bit j is on
bitcount[j]++;
else
bitcount[j]--;
x = 0;
for (i = 0; i < 32; i++)
if (bitcount[i] > 0)
x = x | (1 << i);
return x;
}
int main()
{
int i;
int arr[5] = {1, 3 ,1, 1, 3};
printf(" %d ", findmaj(arr, 5));
getchar();
return 0;
}
We keep a count of frequency of each of the bits. Since majority element will dominate the frequency count, hence we can get its value.
The solution is constant space and linear time : O(n)
Method 4 (Using Binary Search Tree)
Node of the Binary Search Tree (used in this approach) will be as follows. ?
struct tree
{
int element;
int count;
}BST;
Insert elements in BST one by one and if an element is already present then increment the count of the node. At any stage, if count of a node becomes more than n/2 then return.
The method works well for the cases where n/2+1 occurrences of the majority element is present in the starting of the array, for example {1, 1, 1, 1, 1, 2, 3, 4}.
Time Complexity: If a binary search tree is used then time complexity will be O(n^2). If a self-balancing-binary-search tree is used then O(nlogn)
Auxiliary Space: O(n)
METHOD 5 (Using Moore’s Voting Algorithm)
This is a two step process.
1. Get an element occurring most of the time in the array. This phase will make sure that if there is a majority element then it will return that only.
2. Check if the element obtained from above step is majority element.
1. Finding a Candidate:
The algorithm for first phase that works in O(n) is known as Moore’s Voting Algorithm. Basic idea of the algorithm is if we cancel out each occurrence of an element e with all the other elements that are different from e then e will exist till end if it is a majority element.
findCandidate(a[], size)
1. Initialize index and count of majority element
maj_index = 0, count = 1
2. Loop for i = 1 to size – 1
(a)If a[maj_index] == a[i]
count++
(b)Else
count--;
(c)If count == 0
maj_index = i;
count = 1
3. Return a[maj_index]
Above algorithm loops through each element and maintains a count of a[maj_index], If next element is same then increments the count, if next element is not same then decrements the count, and if the count reaches 0 then changes the maj_index to the current element and sets count to 1.
First Phase algorithm gives us a candidate element. In second phase we need to check if the candidate is really a majority element. Second phase is simple and can be easily done in O(n). We just need to check if count of the candidate element is greater than n/2.
Example:
A[] = 2, 2, 3, 5, 2, 2, 6
Initialize:
maj_index = 0, count = 1 –> candidate ‘2?
2, 2, 3, 5, 2, 2, 6
Same as a[maj_index] => count = 2
2, 2, 3, 5, 2, 2, 6
Different from a[maj_index] => count = 1
2, 2, 3, 5, 2, 2, 6
Different from a[maj_index] => count = 0
Since count = 0, change candidate for majority element to 5 => maj_index = 3, count = 1
2, 2, 3, 5, 2, 2, 6
Different from a[maj_index] => count = 0
Since count = 0, change candidate for majority element to 2 => maj_index = 4
2, 2, 3, 5, 2, 2, 6
Same as a[maj_index] => count = 2
2, 2, 3, 5, 2, 2, 6
Different from a[maj_index] => count = 1
Finally candidate for majority element is 2.
First step uses Moore’s Voting Algorithm to get a candidate for majority element.
2. Check if the element obtained in step 1 is majority
printMajority (a[], size)
1. Find the candidate for majority
2. If candidate is majority. i.e., appears more than n/2 times.
Print the candidate
3. Else
Print "NONE"
# include<stdio.h>
# define bool int
int findCandidate(int *, int);
bool isMajority(int *, int, int);
void printMajority(int a[], int size)
{
int cand = findCandidate(a, size);
if(isMajority(a, size, cand))
printf(" %d ", cand);
else
printf("NO Majority Element");
}
int findCandidate(int a[], int size)
{
int maj_index = 0, count = 1;
int i;
for(i = 1; i < size; i++)
{
if(a[maj_index] == a[i])
count++;
else
count--;
if(count == 0)
{
maj_index = i;
count = 1;
}
}
return a[maj_index];
}
bool isMajority(int a[], int size, int cand)
{
int i, count = 0;
for (i = 0; i < size; i++)
if(a[i] == cand)
count++;
if (count > size/2)
return 1;
else
return 0;
}
int main()
{
int a[] = {1, 3, 3, 1,1,1,2,3,1,2,1,1};
printMajority(a, 12);
getchar();
return 0;
}
Time Complexity: O(n)
Auxiliary Space : O(1)
Run Here
Solution 1: A basic solution is to scan entire array for checking for every element in the array. If any element occurs more than n/2 time, prints it and break the loop. This will be of O(n^2) complexity.
Solution 2: Sort the entire array in O(nlogn) and then in one pass keep counting the elements. This will be of O(nlogn) + O() = O(nlogn) complexity. #try it
Solution 3 Using BitCount Array
#include
int findmaj(int arr[], int n)
{
int bitcount[32];
int i, j, x;
for(i = 0; i < 32; i++)
bitcount[i] = 0;
for (i = 0; i < n; i++)
for (j = 0; j < 32; j++)
if (arr[i] & (1 << j)) // if bit j is on
bitcount[j]++;
else
bitcount[j]--;
x = 0;
for (i = 0; i < 32; i++)
if (bitcount[i] > 0)
x = x | (1 << i);
return x;
}
int main()
{
int i;
int arr[5] = {1, 3 ,1, 1, 3};
printf(" %d ", findmaj(arr, 5));
getchar();
return 0;
}
We keep a count of frequency of each of the bits. Since majority element will dominate the frequency count, hence we can get its value.
The solution is constant space and linear time : O(n)
Method 4 (Using Binary Search Tree)
Node of the Binary Search Tree (used in this approach) will be as follows. ?
struct tree
{
int element;
int count;
}BST;
Insert elements in BST one by one and if an element is already present then increment the count of the node. At any stage, if count of a node becomes more than n/2 then return.
The method works well for the cases where n/2+1 occurrences of the majority element is present in the starting of the array, for example {1, 1, 1, 1, 1, 2, 3, 4}.
Time Complexity: If a binary search tree is used then time complexity will be O(n^2). If a self-balancing-binary-search tree is used then O(nlogn)
Auxiliary Space: O(n)
METHOD 5 (Using Moore’s Voting Algorithm)
This is a two step process.
1. Get an element occurring most of the time in the array. This phase will make sure that if there is a majority element then it will return that only.
2. Check if the element obtained from above step is majority element.
1. Finding a Candidate:
The algorithm for first phase that works in O(n) is known as Moore’s Voting Algorithm. Basic idea of the algorithm is if we cancel out each occurrence of an element e with all the other elements that are different from e then e will exist till end if it is a majority element.
findCandidate(a[], size)
1. Initialize index and count of majority element
maj_index = 0, count = 1
2. Loop for i = 1 to size – 1
(a)If a[maj_index] == a[i]
count++
(b)Else
count--;
(c)If count == 0
maj_index = i;
count = 1
3. Return a[maj_index]
Above algorithm loops through each element and maintains a count of a[maj_index], If next element is same then increments the count, if next element is not same then decrements the count, and if the count reaches 0 then changes the maj_index to the current element and sets count to 1.
First Phase algorithm gives us a candidate element. In second phase we need to check if the candidate is really a majority element. Second phase is simple and can be easily done in O(n). We just need to check if count of the candidate element is greater than n/2.
Example:
A[] = 2, 2, 3, 5, 2, 2, 6
Initialize:
maj_index = 0, count = 1 –> candidate ‘2?
2, 2, 3, 5, 2, 2, 6
Same as a[maj_index] => count = 2
2, 2, 3, 5, 2, 2, 6
Different from a[maj_index] => count = 1
2, 2, 3, 5, 2, 2, 6
Different from a[maj_index] => count = 0
Since count = 0, change candidate for majority element to 5 => maj_index = 3, count = 1
2, 2, 3, 5, 2, 2, 6
Different from a[maj_index] => count = 0
Since count = 0, change candidate for majority element to 2 => maj_index = 4
2, 2, 3, 5, 2, 2, 6
Same as a[maj_index] => count = 2
2, 2, 3, 5, 2, 2, 6
Different from a[maj_index] => count = 1
Finally candidate for majority element is 2.
First step uses Moore’s Voting Algorithm to get a candidate for majority element.
2. Check if the element obtained in step 1 is majority
printMajority (a[], size)
1. Find the candidate for majority
2. If candidate is majority. i.e., appears more than n/2 times.
Print the candidate
3. Else
Print "NONE"
# define bool int
int findCandidate(int *, int);
bool isMajority(int *, int, int);
void printMajority(int a[], int size)
{
int cand = findCandidate(a, size);
if(isMajority(a, size, cand))
printf(" %d ", cand);
else
printf("NO Majority Element");
}
int findCandidate(int a[], int size)
{
int maj_index = 0, count = 1;
int i;
for(i = 1; i < size; i++)
{
if(a[maj_index] == a[i])
count++;
else
count--;
if(count == 0)
{
maj_index = i;
count = 1;
}
}
return a[maj_index];
}
bool isMajority(int a[], int size, int cand)
{
int i, count = 0;
for (i = 0; i < size; i++)
if(a[i] == cand)
count++;
if (count > size/2)
return 1;
else
return 0;
}
int main()
{
int a[] = {1, 3, 3, 1,1,1,2,3,1,2,1,1};
printMajority(a, 12);
getchar();
return 0;
}
Auxiliary Space : O(1)
Labels:Data
Amazon Interview
,
Facebook Interview
,
Goldman Sachs Interview
,
Hyves Interview
,
Yahoo Interview
Amplitude of Element In Unsorted Array
/*
The amplitude of a non-empty zero-indexed array A consisting of N numbers is defined as
amplitude(A) = max { A[P] - A[Q] : 0 <= P, Q < N }
Write a function
int amplitude(int[] A);
that given a non-empty zero-indexed array A consisting of N non-negative integers returns its amplitude. Assume that the length of the array does not exceed 1,000,000. Assume that each element of the array is a non-negative integer not exceeding 5,000,000.
For example, given array A such that
A[0]=10, A[1]=2, A[2]=44, A[3]=15, A[4]=39, A[5]=20
the function should return 42.
*/
Java Code
class array
{
public static void main(String a[])
{
System.out.println(amplitude(new int[]{10, 2, 44, 15, 39, 20}));
}
static int amplitude ( int[] A )
{
// write your code here
int min=A[0];
int max=A[0];
int diff=0;
if(A==null)
return 0;
if(A.length==0)
return 0;
if(A.length>1000000)
{
return 0;
}
else
{
for(int i=0;i
if(A[i]
if(A[i]>max)
max=A[i];
diff=max-min;
}
}
return diff;
}
}
The amplitude of a non-empty zero-indexed array A consisting of N numbers is defined as
amplitude(A) = max { A[P] - A[Q] : 0 <= P, Q < N }
Write a function
int amplitude(int[] A);
that given a non-empty zero-indexed array A consisting of N non-negative integers returns its amplitude. Assume that the length of the array does not exceed 1,000,000. Assume that each element of the array is a non-negative integer not exceeding 5,000,000.
For example, given array A such that
A[0]=10, A[1]=2, A[2]=44, A[3]=15, A[4]=39, A[5]=20
the function should return 42.
*/
Java Code
class array
{
public static void main(String a[])
{
System.out.println(amplitude(new int[]{10, 2, 44, 15, 39, 20}));
}
static int amplitude ( int[] A )
{
// write your code here
int min=A[0];
int max=A[0];
int diff=0;
if(A==null)
return 0;
if(A.length==0)
return 0;
if(A.length>1000000)
{
return 0;
}
else
{
for(int i=0;i
if(A[i]
if(A[i]>max)
max=A[i];
diff=max-min;
}
}
return diff;
}
}
Labels:Data
Adobe Question
,
Hyves Interview
Sunday, March 6, 2011
WAPFind nth Fibonacci number Efficiently..its in O(logn)
The Fibonacci numbers are the numbers in the following integer sequence.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 141, ……..
In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation
F(n)=F(n-1)+F(n-2)
Method 1 ( Use recursion )
A simple method that is a direct recursive implementation mathematical recurance relation given above.
#include
int fib(int n)
{
if ( n <= 1 )
return n;
return fib(n-1) + fib(n-2);
}
int main ()
{
int n = 9;
printf("%d", fib(n));
getchar();
return 0;
}
Time Complexity: T(n) = T(n-1) + T(n-2) which is exponential.
We can observe that this implementation does a lot of repeated work (see the following recursion tree). So this is a bad implementation for nth Fibonacci number.
fib(5)
/ \
fib(4) fib(3)
/ \ / \
fib(3) fib(2) fib(2) fib(1)
/ \ / \ / \
fib(2) fib(1) fib(1) fib(0) fib(1) fib(0)
/ \
fib(1) fib(0)
Extra Space: O(n) if we consider the fuinction call stack size, otherwise O(1).
Method 2 ( Use Dynamic Programming )
We can avoid the repeated work done is the method 1 by storing the Fibonacci numbers calculated so far.
?
#include
int fib(int n)
{
/* Declare an array to store fibonacci numbers. */
int f[n+1];
int i;
/* 0th and 1st number of the series are 0 and 1*/
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
{
/* Add the previous 2 numbers in the series
and store it */
f[i] = f[i-1] + f[i-2];
}
return f[n];
}
int main ()
{
int n = 9;
printf("%d", fib(n));
getchar();
return 0;
}
Time Complexity: O(n)
Extra Space: O(n)
Method 3 ( Space Otimized Method 2 )
We can optimize the space used in method 2 by storing the previous two numbers only because that is all we need to get the next Fibannaci number in series.
?
#include
int fib(int n)
{
int a = 0, b = 1, c, i;
if( n == 0)
return a;
for (i = 2; i <= n; i++)
{
c = a + b;
a = b;
b = c;
}
return b;
}
int main ()
{
int n = 9;
printf("%d", fib(n));
getchar();
return 0;
}
Time Complexity: O(n)
Extra Space: O(1)
here another O(n) which relies on the fact that if we n times multiply the matrix M = {{1,0},{0,1}} to itself (in other words calculate power(M, n )), then we get the (n+1)th Fibonacci number as the element at 0,0 in the resultant matrix.
The matrix representation gives the following closed expression for the Fibonacci numbers:
1 1 ^n = Fn+1 Fn
1 0 Fn Fn-1
#include
/* Helper function that multiplies 2 matricies F and M of size 2*2, and
puts the multiplication result back to F[][] */
void multiply(int F[2][2], int M[2][2]);
/* Helper function that calculates F[][] raise to the power n and puts the
result in F[][]
Note that this function is desinged only for fib() and won't work as general
power function */
void power(int F[2][2], int n);
/* Helper function that multiplies 2 matricies F and M of size 2*2, and puts
the multiplication result back to F[][] */
void multiply(int F[2][2], int M[2][2]);
int fib(int n)
{
int F[2][2] = {{1,1},{1,0}};
if(n == 0)
return 0;
power(F, n-1);
return F[0][0];
}
void multiply(int F[2][2], int M[2][2])
{
int x = F[0][0]*M[0][0] + F[0][1]*M[1][0];
int y = F[0][0]*M[0][1] + F[0][1]*M[1][1];
int z = F[1][0]*M[0][0] + F[1][1]*M[1][0];
int w = F[1][0]*M[0][1] + F[1][1]*M[1][1];
F[0][0] = x;
F[0][1] = y;
F[1][0] = z;
F[1][1] = w;
}
void power(int F[2][2], int n)
{
int i;
int M[2][2] = {{1,1},{1,0}};
// n - 1 times multiply the matrix to {{1,0},{0,1}}
for ( i = 2; i <= n; i++ )
multiply(F, M);
}
/* Driver program to test above function */
int main()
{
int n = 9;
printf("%d", fib(n));
getchar();
return 0;
}
Time Complexity: O(n)
Extra Space: O(1)
Method 5 ( Optimized Method 4 )
The method 4 can be optimized to work in O(Logn) time complexity. We can do recursive multiplication to get power(M, n) in the prevous method (Similar to the optimization done in this post)
?
#include
void multiply(int F[2][2], int M[2][2]);
void power(int F[2][2], int n);
/* function that returns nth Fibonacci number */
int fib(int n)
{
int F[2][2] = {{1,1},{1,0}};
if(n == 0)
return 0;
power(F, n-1);
return F[0][0];
}
/* Optimized version of power() in method 4 */
void power(int F[2][2], int n)
{
if( n == 1 )
return;
int M[2][2] = {{1,1},{1,0}};
power(F, n/2);
multiply(F, F);
if( n%2 != 0 )
multiply(F, M);
}
void multiply(int F[2][2], int M[2][2])
{
int x = F[0][0]*M[0][0] + F[0][1]*M[1][0];
int y = F[0][0]*M[0][1] + F[0][1]*M[1][1];
int z = F[1][0]*M[0][0] + F[1][1]*M[1][0];
int w = F[1][0]*M[0][1] + F[1][1]*M[1][1];
F[0][0] = x;
F[0][1] = y;
F[1][0] = z;
F[1][1] = w;
}
/* Driver program to test above function */
int main()
{
int n = 9;
printf("%d", fib(9));
getchar();
return 0;
}
Time Complexity: O(Logn)
Extra Space: O(Logn) if we consider the function call stack size, otherwise O(1).
Follow Up
WAP For Generating The Series of Fibonacci Numbers . More Focused on Time & Space Complexity
As a simple rule of recursion, any function can be computed using a recursive routine if :
1. The function can be expressed in its own form.
2. There exists a termination step, the point at which f(x) is known for a particular ‘x’.
Therefore to write a recursive program to find the nth term of the fibonacci series, we have to express the fibonacci sequence in a recursive form using the above 2 rules :
1. fib(n) = fib(n-1) + fib(n-2) (recursive defination of fibonacci series).
2. if n=0 or n=1, return n (termination step).
Using these 2 rules, the recursive program for finding the nth term of the fibonacci series can be coded very easily as shown.
The exe file can be downloaded from here : FIBONACCI
#include "stdio.h"
int fib(int n)
{
if(n==1 || n==0)
return n;
return fib(n-1)+fib(n-2);
}
int main()
{
int i,r;
for(i=0;i<10;i++)
{
r=fib(i);
printf("%d %d \n",i,r);
}
return 0;
}
Here is Time Complexity Explanation as We Know Fibonacci series is like
0, 1, 1, 2, 3, 5, 8, 13, ...& so on
start form this position
fib(0)=1
fib(1)=2
fib(2) = fib(0) + fib (1) // 1 + 1 + 1 = 3 = 2^1 + 1
fib(3) = fib(1) + fib (2) // 1 + 3 + 1 = 5 = 2^2 + 1
fib(4) = fib(2) + fib(3) // 3 + 5 + 1 = 9 = 2^3 + 1
hence fib(n) - recursive calls = 2^(n-1) + 1
So O(2^n) - which is exponential complexity. Looking at the space in similar fashion for each recursive call - we get O(n)
Time Complexity O(2^n)
Space Complexity O(n)
Run Here https://ideone.com/1RlcP
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 141, ……..
In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation
F(n)=F(n-1)+F(n-2)
Method 1 ( Use recursion )
A simple method that is a direct recursive implementation mathematical recurance relation given above.
#include
int fib(int n)
{
if ( n <= 1 )
return n;
return fib(n-1) + fib(n-2);
}
int main ()
{
int n = 9;
printf("%d", fib(n));
getchar();
return 0;
}
Time Complexity: T(n) = T(n-1) + T(n-2) which is exponential.
We can observe that this implementation does a lot of repeated work (see the following recursion tree). So this is a bad implementation for nth Fibonacci number.
fib(5)
/ \
fib(4) fib(3)
/ \ / \
fib(3) fib(2) fib(2) fib(1)
/ \ / \ / \
fib(2) fib(1) fib(1) fib(0) fib(1) fib(0)
/ \
fib(1) fib(0)
Extra Space: O(n) if we consider the fuinction call stack size, otherwise O(1).
Method 2 ( Use Dynamic Programming )
We can avoid the repeated work done is the method 1 by storing the Fibonacci numbers calculated so far.
?
#include
int fib(int n)
{
/* Declare an array to store fibonacci numbers. */
int f[n+1];
int i;
/* 0th and 1st number of the series are 0 and 1*/
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
{
/* Add the previous 2 numbers in the series
and store it */
f[i] = f[i-1] + f[i-2];
}
return f[n];
}
int main ()
{
int n = 9;
printf("%d", fib(n));
getchar();
return 0;
}
Time Complexity: O(n)
Extra Space: O(n)
Method 3 ( Space Otimized Method 2 )
We can optimize the space used in method 2 by storing the previous two numbers only because that is all we need to get the next Fibannaci number in series.
?
#include
int fib(int n)
{
int a = 0, b = 1, c, i;
if( n == 0)
return a;
for (i = 2; i <= n; i++)
{
c = a + b;
a = b;
b = c;
}
return b;
}
int main ()
{
int n = 9;
printf("%d", fib(n));
getchar();
return 0;
}
Time Complexity: O(n)
Extra Space: O(1)
here another O(n) which relies on the fact that if we n times multiply the matrix M = {{1,0},{0,1}} to itself (in other words calculate power(M, n )), then we get the (n+1)th Fibonacci number as the element at 0,0 in the resultant matrix.
The matrix representation gives the following closed expression for the Fibonacci numbers:
1 1 ^n = Fn+1 Fn
1 0 Fn Fn-1
#include
/* Helper function that multiplies 2 matricies F and M of size 2*2, and
puts the multiplication result back to F[][] */
void multiply(int F[2][2], int M[2][2]);
/* Helper function that calculates F[][] raise to the power n and puts the
result in F[][]
Note that this function is desinged only for fib() and won't work as general
power function */
void power(int F[2][2], int n);
/* Helper function that multiplies 2 matricies F and M of size 2*2, and puts
the multiplication result back to F[][] */
void multiply(int F[2][2], int M[2][2]);
int fib(int n)
{
int F[2][2] = {{1,1},{1,0}};
if(n == 0)
return 0;
power(F, n-1);
return F[0][0];
}
void multiply(int F[2][2], int M[2][2])
{
int x = F[0][0]*M[0][0] + F[0][1]*M[1][0];
int y = F[0][0]*M[0][1] + F[0][1]*M[1][1];
int z = F[1][0]*M[0][0] + F[1][1]*M[1][0];
int w = F[1][0]*M[0][1] + F[1][1]*M[1][1];
F[0][0] = x;
F[0][1] = y;
F[1][0] = z;
F[1][1] = w;
}
void power(int F[2][2], int n)
{
int i;
int M[2][2] = {{1,1},{1,0}};
// n - 1 times multiply the matrix to {{1,0},{0,1}}
for ( i = 2; i <= n; i++ )
multiply(F, M);
}
/* Driver program to test above function */
int main()
{
int n = 9;
printf("%d", fib(n));
getchar();
return 0;
}
Time Complexity: O(n)
Extra Space: O(1)
Method 5 ( Optimized Method 4 )
The method 4 can be optimized to work in O(Logn) time complexity. We can do recursive multiplication to get power(M, n) in the prevous method (Similar to the optimization done in this post)
?
#include
void multiply(int F[2][2], int M[2][2]);
void power(int F[2][2], int n);
/* function that returns nth Fibonacci number */
int fib(int n)
{
int F[2][2] = {{1,1},{1,0}};
if(n == 0)
return 0;
power(F, n-1);
return F[0][0];
}
/* Optimized version of power() in method 4 */
void power(int F[2][2], int n)
{
if( n == 1 )
return;
int M[2][2] = {{1,1},{1,0}};
power(F, n/2);
multiply(F, F);
if( n%2 != 0 )
multiply(F, M);
}
void multiply(int F[2][2], int M[2][2])
{
int x = F[0][0]*M[0][0] + F[0][1]*M[1][0];
int y = F[0][0]*M[0][1] + F[0][1]*M[1][1];
int z = F[1][0]*M[0][0] + F[1][1]*M[1][0];
int w = F[1][0]*M[0][1] + F[1][1]*M[1][1];
F[0][0] = x;
F[0][1] = y;
F[1][0] = z;
F[1][1] = w;
}
/* Driver program to test above function */
int main()
{
int n = 9;
printf("%d", fib(9));
getchar();
return 0;
}
Time Complexity: O(Logn)
Extra Space: O(Logn) if we consider the function call stack size, otherwise O(1).
Follow Up
WAP For Generating The Series of Fibonacci Numbers . More Focused on Time & Space Complexity
As a simple rule of recursion, any function can be computed using a recursive routine if :
1. The function can be expressed in its own form.
2. There exists a termination step, the point at which f(x) is known for a particular ‘x’.
Therefore to write a recursive program to find the nth term of the fibonacci series, we have to express the fibonacci sequence in a recursive form using the above 2 rules :
1. fib(n) = fib(n-1) + fib(n-2) (recursive defination of fibonacci series).
2. if n=0 or n=1, return n (termination step).
Using these 2 rules, the recursive program for finding the nth term of the fibonacci series can be coded very easily as shown.
The exe file can be downloaded from here : FIBONACCI
#include "stdio.h"
int fib(int n)
{
if(n==1 || n==0)
return n;
return fib(n-1)+fib(n-2);
}
int main()
{
int i,r;
for(i=0;i<10;i++)
{
r=fib(i);
printf("%d %d \n",i,r);
}
return 0;
}
Here is Time Complexity Explanation as We Know Fibonacci series is like
0, 1, 1, 2, 3, 5, 8, 13, ...& so on
start form this position
fib(0)=1
fib(1)=2
fib(2) = fib(0) + fib (1) // 1 + 1 + 1 = 3 = 2^1 + 1
fib(3) = fib(1) + fib (2) // 1 + 3 + 1 = 5 = 2^2 + 1
fib(4) = fib(2) + fib(3) // 3 + 5 + 1 = 9 = 2^3 + 1
hence fib(n) - recursive calls = 2^(n-1) + 1
So O(2^n) - which is exponential complexity. Looking at the space in similar fashion for each recursive call - we get O(n)
Time Complexity O(2^n)
Space Complexity O(n)
Run Here https://ideone.com/1RlcP
Labels:Data
Amazon Interview
,
Facebook Interview
,
Google Interview
,
Hyves Interview
,
Microsoft Interview
Thursday, February 24, 2011
WAP to Convert Zig Zag level order Traversal of Tree to Doubly Linked List
Method 1 using 2-Stack--Need Modification RunTime Error But Logic is 100% Correct
#include
#include
/* Structure for Tree */
struct node
{
struct node* left;
struct node* right;
int data;
};
/* structure of a stack node */
struct sNode
{
struct node *t;
struct sNode *next;
};
/* Helper function that allocates a new tNode with the
given data and NULL left and right pointers. */
struct node* newtNode(int data)
{
struct node* node = (struct node*)
malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
/* UTILITY FUNCTIONS */
/* Function to push an item to sNode*/
void push(struct sNode** top_ref, struct node *t)
{
/* allocate tNode */
struct sNode* new_tNode =
(struct sNode*) malloc(sizeof(struct sNode));
if(new_tNode == NULL)
{
printf("Stack Overflow \n");
getchar();
exit(0);
}
/* put in the data */
new_tNode->t = t;
/* link the old list off the new tNode */
new_tNode->next = (*top_ref);
/* move the head to point to the new tNode */
(*top_ref) = new_tNode;
}
/* The function returns true if stack is empty, otherwise false */
bool isEmpty(struct sNode *top)
{
return (top == NULL)? 1 : 0;
}
/* Function to pop an item from stack*/
struct node *pop(struct sNode** top_ref)
{
struct node *res;
struct sNode *top;
/*If sNode is empty then error */
if(isEmpty(*top_ref))
{
printf("Stack Underflow \n");
getchar();
exit(0);
}
else
{
top = *top_ref;
res = top->t;
*top_ref = top->next;
free(top);
return res;
}
}
void Insert(struct node** head_ref, int new_data)
{
/* allocate node */
struct node* new_node =
(struct node*) malloc(sizeof(struct node));
/* put in the data */
new_node->data = new_data;
/* since we are adding at the begining,
prev is always NULL */
new_node->left= NULL;
/* link the old list off the new node */
new_node->right= (*head_ref);
/* change prev of head node to new node */
if((*head_ref) != NULL)
(*head_ref)->left= new_node ;
/* move the head to point to the new node */
(*head_ref) = new_node;
}
void Spiral(struct node* root)
{
struct node *head;//for DLL
struct sNode *node1;
struct sNode *node2;
struct node *temp;
if(root == NULL)
return;
push(&node1,root);
while(!isEmpty(node1) && !isEmpty(node2))
{
while(!isEmpty(node1))
{
temp = pop(&node1);
Insert(&head,temp->data);
push(&node2,temp->right);
push(&node2,temp->left);
}
//temp=NULL;
while(!isEmpty(node2))
{
temp = pop(&node2);
Insert(&head,temp->data);
push(&node1,temp -> left);
push(&node1,temp -> right);
}
}
}
/* Given a binary tree, print its nodes in inorder*/
void printInorder(struct node* node)
{
if (node == NULL)
return;
/* first recur on left child */
printInorder(node->left);
/* then print the data of node */
printf("%d ", node->data);
/* now recur on right child */
printInorder(node->right);
}
/* Utility function to print a linked list */
void printList(struct node* head)
{
while(head!=NULL)
{
printf("%d ",head->data);
head=head->right;
}
printf("\n");
}
/* Driver function to test above functions */
int main()
{
struct node *root = newtNode(1);
root->left = newtNode(2);
root->right = newtNode(3);
root->left->left = newtNode(4);
root->left->right = newtNode(5);
root->right->left = newtNode(6);
root->right->right = newtNode(7);
Spiral(root);
printList(root);
getchar();
}
TC O(n)
Sc (2n) if Stack Space is considered else O(1)
Run Here https://ideone.com/cyPM5
Method 2 Using Recursion(Bottom Up Tree Traversal)
#include
#include
struct node
{
struct node *left;
struct node *right;
int data;
};
struct node *rslt;//Global structure pointer..it point to head of doubly linked list
int height(struct node* head)
{
if(head==NULL)
return 0;
if(head->left==NULL && head->right==NULL)
return 0;
int lh=height(head->left);
int rh=height(head->right);
return lh>rh?(lh+1):(rh+1);
}
struct node* appnd(struct node *a,struct node *b)
{
if(a==NULL)return b;
if(b==NULL)return a;
struct node* result=a;
while(a->left!=NULL)
a=a->left;
a->left=b;
b->right=a;
b->left=NULL;
return result;
}
void printGivenLevel(struct node* head,int level,int ltr)
{
if(head==NULL)
return;
if(level==0)
{
appnd(rslt, head);
rslt = head;
}
if(level>0)
{
if(ltr)
{
printGivenLevel(head->left,level-1,ltr);
printGivenLevel(head->right,level-1,ltr);
}
else
{
printGivenLevel(head->right,level-1,ltr);
printGivenLevel(head->left,level-1,ltr);
}
}
}
void printGivenOrder(struct node* head)
{
int i=0;
int ltr=0;
for(i=height(head); i >= 0; i--)
{
printGivenLevel(head,i,ltr);
ltr=~ltr;
}
}
struct node* NewNode(int data)
{
struct node* tmp=(struct node *)malloc(sizeof(struct node));
tmp->data=data;
tmp->left=NULL;
tmp->right=NULL;
return tmp;
}
void printList(struct node* node)
{
struct node* current=node;
while(current)
{
printf("%d ----> ",current->data);
current=current->right;
}
}
int main()
{
struct node* start=NULL;
start=NewNode(1);
start->left=NewNode(2);
start->right=NewNode(3);
start->left->left=NewNode(4);
start->left->right=NewNode(5);
start->right->left=NewNode(6);
start->right->right=NewNode(7);
printGivenOrder(start);
printList(rslt);
return 0;
}
TC O(n^2)....need Modification..??
Sc O(1)
Run Here https://ideone.com/y9Ssb
#include
#include
/* Structure for Tree */
struct node
{
struct node* left;
struct node* right;
int data;
};
/* structure of a stack node */
struct sNode
{
struct node *t;
struct sNode *next;
};
/* Helper function that allocates a new tNode with the
given data and NULL left and right pointers. */
struct node* newtNode(int data)
{
struct node* node = (struct node*)
malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
/* UTILITY FUNCTIONS */
/* Function to push an item to sNode*/
void push(struct sNode** top_ref, struct node *t)
{
/* allocate tNode */
struct sNode* new_tNode =
(struct sNode*) malloc(sizeof(struct sNode));
if(new_tNode == NULL)
{
printf("Stack Overflow \n");
getchar();
exit(0);
}
/* put in the data */
new_tNode->t = t;
/* link the old list off the new tNode */
new_tNode->next = (*top_ref);
/* move the head to point to the new tNode */
(*top_ref) = new_tNode;
}
/* The function returns true if stack is empty, otherwise false */
bool isEmpty(struct sNode *top)
{
return (top == NULL)? 1 : 0;
}
/* Function to pop an item from stack*/
struct node *pop(struct sNode** top_ref)
{
struct node *res;
struct sNode *top;
/*If sNode is empty then error */
if(isEmpty(*top_ref))
{
printf("Stack Underflow \n");
getchar();
exit(0);
}
else
{
top = *top_ref;
res = top->t;
*top_ref = top->next;
free(top);
return res;
}
}
void Insert(struct node** head_ref, int new_data)
{
/* allocate node */
struct node* new_node =
(struct node*) malloc(sizeof(struct node));
/* put in the data */
new_node->data = new_data;
/* since we are adding at the begining,
prev is always NULL */
new_node->left= NULL;
/* link the old list off the new node */
new_node->right= (*head_ref);
/* change prev of head node to new node */
if((*head_ref) != NULL)
(*head_ref)->left= new_node ;
/* move the head to point to the new node */
(*head_ref) = new_node;
}
void Spiral(struct node* root)
{
struct node *head;//for DLL
struct sNode *node1;
struct sNode *node2;
struct node *temp;
if(root == NULL)
return;
push(&node1,root);
while(!isEmpty(node1) && !isEmpty(node2))
{
while(!isEmpty(node1))
{
temp = pop(&node1);
Insert(&head,temp->data);
push(&node2,temp->right);
push(&node2,temp->left);
}
//temp=NULL;
while(!isEmpty(node2))
{
temp = pop(&node2);
Insert(&head,temp->data);
push(&node1,temp -> left);
push(&node1,temp -> right);
}
}
}
/* Given a binary tree, print its nodes in inorder*/
void printInorder(struct node* node)
{
if (node == NULL)
return;
/* first recur on left child */
printInorder(node->left);
/* then print the data of node */
printf("%d ", node->data);
/* now recur on right child */
printInorder(node->right);
}
/* Utility function to print a linked list */
void printList(struct node* head)
{
while(head!=NULL)
{
printf("%d ",head->data);
head=head->right;
}
printf("\n");
}
/* Driver function to test above functions */
int main()
{
struct node *root = newtNode(1);
root->left = newtNode(2);
root->right = newtNode(3);
root->left->left = newtNode(4);
root->left->right = newtNode(5);
root->right->left = newtNode(6);
root->right->right = newtNode(7);
Spiral(root);
printList(root);
getchar();
}
TC O(n)
Sc (2n) if Stack Space is considered else O(1)
Run Here https://ideone.com/cyPM5
Method 2 Using Recursion(Bottom Up Tree Traversal)
#include
#include
struct node
{
struct node *left;
struct node *right;
int data;
};
struct node *rslt;//Global structure pointer..it point to head of doubly linked list
int height(struct node* head)
{
if(head==NULL)
return 0;
if(head->left==NULL && head->right==NULL)
return 0;
int lh=height(head->left);
int rh=height(head->right);
return lh>rh?(lh+1):(rh+1);
}
struct node* appnd(struct node *a,struct node *b)
{
if(a==NULL)return b;
if(b==NULL)return a;
struct node* result=a;
while(a->left!=NULL)
a=a->left;
a->left=b;
b->right=a;
b->left=NULL;
return result;
}
void printGivenLevel(struct node* head,int level,int ltr)
{
if(head==NULL)
return;
if(level==0)
{
appnd(rslt, head);
rslt = head;
}
if(level>0)
{
if(ltr)
{
printGivenLevel(head->left,level-1,ltr);
printGivenLevel(head->right,level-1,ltr);
}
else
{
printGivenLevel(head->right,level-1,ltr);
printGivenLevel(head->left,level-1,ltr);
}
}
}
void printGivenOrder(struct node* head)
{
int i=0;
int ltr=0;
for(i=height(head); i >= 0; i--)
{
printGivenLevel(head,i,ltr);
ltr=~ltr;
}
}
struct node* NewNode(int data)
{
struct node* tmp=(struct node *)malloc(sizeof(struct node));
tmp->data=data;
tmp->left=NULL;
tmp->right=NULL;
return tmp;
}
void printList(struct node* node)
{
struct node* current=node;
while(current)
{
printf("%d ----> ",current->data);
current=current->right;
}
}
int main()
{
struct node* start=NULL;
start=NewNode(1);
start->left=NewNode(2);
start->right=NewNode(3);
start->left->left=NewNode(4);
start->left->right=NewNode(5);
start->right->left=NewNode(6);
start->right->right=NewNode(7);
printGivenOrder(start);
printList(rslt);
return 0;
}
TC O(n^2)....need Modification..??
Sc O(1)
Run Here https://ideone.com/y9Ssb
Labels:Data
Amazon Interview
,
Facebook Interview
,
Google Interview
,
Hyves Interview
Tuesday, February 22, 2011
WAP for Quick Sort Algorithm
Data Structure used:Array
Algorithm:Divide & Conquer
1. Phase:Partition O(N) Time
2. Phase: Divide the array in two part Recursively & call partition function until we are run out of array O(nlogn)
Recursive Function Looks Like T(n)=2*T(n/2)+O(n)
Working Code:
public class QuickSort
{
public static int SIZE = 1000000;
public int[] sort(int[] input) {
quickSort(input, 0, input.length-1);
return input;
}
public static void main(String args[]){
int[] a = new int[SIZE];
for(int i=0;i pivot)
j--;
if (i <= j) {
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
}
return i;
}
}
//Time taken to sort a million elements : 156 milliseconds
Time Complexity O(nlogn)
Space Complexity O(logn)
Run Here http://ideone.com/clone/ClBCZ
Complexity Analysis ( More Focus on Space )
very Few of us Know & are abale to come up space compelxity of quick sort if asked during the interview isn't it ?
Quicksort has a space complexity of O(logn), even in the worst case, when it is carefully implemented such that
* in-place partitioning is used. This requires O(1).
* After partitioning, the partition with the fewest elements is (recursively) sorted first, requiring at most O(logn) space. Then the other partition is sorted using tail-recursion or iteration.
The version of quicksort with in-place partitioning uses only constant additional space before making any recursive call. However, if it has made O(logn) nested recursive calls, it needs to store a constant amount of information from each of them. Since the best case makes at most O(logn) nested recursive calls, it uses O(logn) space. The worst case makes O(n) nested recursive calls, and so needs O(n) space.
However, if we consider sorting arbitrarily large lists, we have to keep in mind that our variables like left and right can no longer be considered to occupy constant space; it takes O(logn) bits to index into a list of n items. Because we have variables like this in every stack frame, in reality quicksort requires O(log2n) bits of space in the best and average case and O(nlogn) space in the worst case. This isn't too terrible, though, since if the list contains mostly distinct elements, the list itself will also occupy O(nlogn) bits of space.
Algorithm:Divide & Conquer
1. Phase:Partition O(N) Time
2. Phase: Divide the array in two part Recursively & call partition function until we are run out of array O(nlogn)
Recursive Function Looks Like T(n)=2*T(n/2)+O(n)
Working Code:
public class QuickSort
{
public static int SIZE = 1000000;
public int[] sort(int[] input) {
quickSort(input, 0, input.length-1);
return input;
}
public static void main(String args[]){
int[] a = new int[SIZE];
for(int i=0;i
j--;
if (i <= j) {
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
}
return i;
}
}
//Time taken to sort a million elements : 156 milliseconds
Time Complexity O(nlogn)
Space Complexity O(logn)
Run Here http://ideone.com/clone/ClBCZ
Complexity Analysis ( More Focus on Space )
very Few of us Know & are abale to come up space compelxity of quick sort if asked during the interview isn't it ?
Quicksort has a space complexity of O(logn), even in the worst case, when it is carefully implemented such that
* in-place partitioning is used. This requires O(1).
* After partitioning, the partition with the fewest elements is (recursively) sorted first, requiring at most O(logn) space. Then the other partition is sorted using tail-recursion or iteration.
The version of quicksort with in-place partitioning uses only constant additional space before making any recursive call. However, if it has made O(logn) nested recursive calls, it needs to store a constant amount of information from each of them. Since the best case makes at most O(logn) nested recursive calls, it uses O(logn) space. The worst case makes O(n) nested recursive calls, and so needs O(n) space.
However, if we consider sorting arbitrarily large lists, we have to keep in mind that our variables like left and right can no longer be considered to occupy constant space; it takes O(logn) bits to index into a list of n items. Because we have variables like this in every stack frame, in reality quicksort requires O(log2n) bits of space in the best and average case and O(nlogn) space in the worst case. This isn't too terrible, though, since if the list contains mostly distinct elements, the list itself will also occupy O(nlogn) bits of space.
Labels:Data
Adobe Question
,
D.E Shaw
,
Facebook Interview
,
Google Interview
,
Hyves Interview
,
Microsoft Interview
,
Sorting Algorithms
,
Yahoo Interview
Subscribe to:
Comments
(
Atom
)
