Find Number of Nodes on the Longest Path in Binary Tree so one thing is sure that this path comprises on two leaves with maximum distance in BT..isn't it
Finding The Longest Path in Binary Tree will use the algorithms used by Diameter of Tree
PS:Don't confused with finding the maximum distance between two nodes in Binary Tree
its completely different algorithm & it has also been solved so u can search in blog.
Algorithm Used to Calculate Diameter/ finding two nodes which are separated by maximum difference.
The diameter of a tree (sometimes called the width) is the number of nodes on the longest path between two leaves in the tree. The diagram below shows two trees each with same 7 as a diameter but different orientation. (also note that there is more than one path in each tree of length nine, but no path longer than nine nodes).

Diameter 7
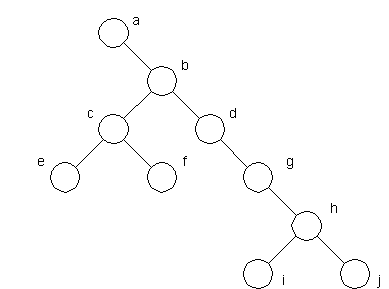
Diameter 7
The diameter of a tree T is the largest of the following quantities:
1 the diameter of T’s left subtree
2 the diameter of T’s right subtree
3 the longest path between leaves that goes through the root of T (this can be computed from the heights of the subtrees of T)
#include
#include
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node
{
int data;
struct node* left;
struct node* right;
};
/* function to create a new node of tree and returns pointer */
struct node* newNode(int data);
/* returns max of two integers */
int max(int a, int b);
/* The function Compute the "height" of a tree. Height is the
number f nodes along the longest path from the root node
down to the farthest leaf node.*/
int height(struct node* node)
{
/* base case tree is empty */
if(node == NULL)
return 0;
/* If tree is not empty then height = 1 + max of left
height and right heights */
return 1 + max(height(node->left), height(node->right));
}
/* Function to get diameter of a binary tree */
int diameter(struct node * tree)
{
/* base case where tree is empty */
if (tree == 0)
return 0;
/* get the height of left and right sub-trees */
int lheight = height(tree->left);
int rheight = height(tree->right);
/* get the diameter of left and right sub-trees */
int ldiameter = diameter(tree->left);
int rdiameter = diameter(tree->right);
/* Return max of following three
1) Diameter of left subtree
2) Diameter of right subtree
3) Height of left subtree + height of right subtree + 1 */
return max(lheight + rheight + 1, max(ldiameter, rdiameter));
}
/* UTILITY FUNCTIONS TO TEST diameter() FUNCTION */
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode(int data)
{
struct node* node = (struct node*)
malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
/* returns maximum of two integers */
int max(int a, int b)
{
return (a >= b)? a: b;
}
/* Driver program to test above functions*/
int main()
{
/* Constructed binary tree is
1 D=4 lh=2,rh=1
/ \
D=3,rh=1 2 3
lh=1 / \
4 5 D=1,lh=rh=0
*/
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf("Diameter of the given binary tree is %d\n", diameter(root));
getchar();
return 0;
}
Time Complexity (N^2)
Space Complexity O(1)
Run Here https://ideone.com/s9OdR
Optimization(2nd Method)
The above implementation can be optimized by calculating the height in the same recursion rather than calling a height() separately. This optimization reduces time complexity to O(n).
#include
#include
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node
{
int data;
struct node* left;
struct node* right;
};
/* function to create a new node of tree and returns pointer */
struct node* newNode(int data);
/* UTILITY FUNCTIONS TO TEST diameter() FUNCTION */
/*The second parameter is to store the height of tree.
Initially, we need to pass a pointer to a location with value
as 0. So, function should be used as follows:
int height = 0;
struct node *root = SomeFunctionToMakeTree();
int diameter = diameterOpt(root, &height); */
int diameterOpt(struct node *root, int* height)
{
/* lh --> Height of left subtree
rh --> Height of right subtree */
int lh = 0, rh = 0;
/* ldiameter --> diameter of left subtree
rdiameter --> Diameter of right subtree */
int ldiameter = 0, rdiameter = 0;
if(root == NULL)
{
*height = 0;
return 0; /* diameter is also 0 */
}
/* Get the heights of left and right subtrees in lh and rh
And store the returned values in ldiameter and ldiameter */
ldiameter = diameterOpt(root->left, &lh);
rdiameter = diameterOpt(root->right, &rh);
/* Height of current node is max of heights of left and
right subtrees plus 1*/
*height = max(lh, rh) + 1;
return max(lh + rh + 1, max(ldiameter, rdiameter));
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode(int data)
{
struct node* node = (struct node*)
malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
/* returns maximum of two integers */
int max(int a, int b)
{
return (a >= b)? a: b;
}
/* Driver program to test above functions*/
int main()
{
/* Constructed binary tree is
1
/ \
2 3
/ \
4 5
*/
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
int height=0;
printf("Diameter of the given binary tree is %d\n", diameter(root,&height));
getchar();
return 0;
}
Time Complexity O(n)
Space Complexity O(1)
Run Here https://ideone.com/uSPq0
More Info http://www.cs.duke.edu/courses/spring00/cps100/assign/trees/diameter.html
![]()




No comments :
Post a Comment